题目内容
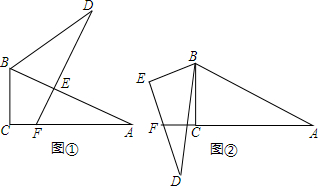
7.已知Rt△ABC≌Rt△DBE,∠ACB=∠DEB=90°,∠A=∠D.(1)将两三角形按图①方式摆放,其中点E落在AB上,DE所在直线交边AC于点F.求证:AF+EF=DE;
(2)若将两三角形按照图②方式摆放,边AC的延长线与DE相交于点F.你认为(1)中的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
分析 (1)由Rt△ABC≌Rt△DBE推出BC=BE,连接BF,根据HL证Rt△BCF≌Rt△BEF,推出CF=EF即可;
(2)猜想(1)结论不成立,关系式是AF=EF+DE,连接BF,根据HL证Rt△BEF≌Rt△BCF,推出EF=FC,由AF=AC+FC可推出AF=DE+EF.
解答 (1)证明:由Rt△ABC≌Rt△DBE知:BC=BE.
连接BF.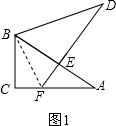
∵在Rt△BCF和Rt△BEF中
$\left\{\begin{array}{l}{BC=BE}\\{BF=BF}\end{array}\right.$,
∴Rt△BCF≌Rt△BEF(HL),
∴CF=EF,
∵AC=DE,CF+FA=CA,
∴AF+EF=DE;
(2)解:(1)中猜想结论不成立,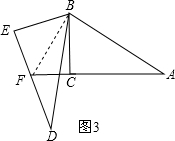 关系式是AF=EF+DE.理由是:
关系式是AF=EF+DE.理由是:
连接BF.
在Rt△BEF和Rt△BCF中
$\left\{\begin{array}{l}{BE=BC}\\{BF=BF}\end{array}\right.$,
∴Rt△BEF≌Rt△BCF(HL),
∴EF=FC,
∵AC=DE,
由AF=AC+FC知:AF=DE+EF.
点评 本题考查了全等三角形的判定和性质,通过构建全等三角形来得出简单的线段相等是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
18.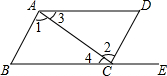 如图,给出下列条件:其中,能推出AB∥DC的是( )
如图,给出下列条件:其中,能推出AB∥DC的是( )
①∠1=∠2; ②∠3=∠4;
③∠B=∠DCE; ④AD∥BC且∠B=∠D.
 如图,给出下列条件:其中,能推出AB∥DC的是( )
如图,给出下列条件:其中,能推出AB∥DC的是( )①∠1=∠2; ②∠3=∠4;
③∠B=∠DCE; ④AD∥BC且∠B=∠D.
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
2.二元一次方程组$\left\{\begin{array}{l}{3x+2y=10}\\{kx+(k+2)y=6}\end{array}\right.$的解x,y的值相等,则k的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{5}{2}$ |
12.下列长度的各组线段能组成一个直角三角形的是( )
| A. | 4cm、5cm、11cm | B. | 4cm、5cm、8cm | C. | $\sqrt{3}$cm、$\sqrt{2}$cm、$\sqrt{5}$cm | D. | 2cm、3cm、6cm |
17. 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
 一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中的两个不等式的解集如图所示,则这个不等式组的解集为( )| A. | -1<x≤2 | B. | -1≤x<2 | C. | -1<x<2 | D. | 无解 |
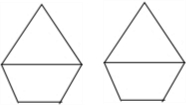 如图是由一个等腰梯形和一个等腰三角形组成的轴对称图形,请你用两种方法作出它的对称轴.(要求:只能用没有刻度的直尺,可不写作法,但要保留作图痕迹)
如图是由一个等腰梯形和一个等腰三角形组成的轴对称图形,请你用两种方法作出它的对称轴.(要求:只能用没有刻度的直尺,可不写作法,但要保留作图痕迹)