题目内容
17.先化简,再求值:(1)(x+y)2-4xy,其中x=12,y=9.
(2)(2a+b)(2a-b)+b(2a+b)-4a2,其中a=-$\frac{1}{2}$,b=2.
分析 (1)利用完全平方公式计算和因式分解,进一步代入求得答案即可;
(2)利用整式的乘法和平方差公式计算,进一步代入求得答案即可.
解答 解:(1)原式=x2+2xy+y2-4xy
=(x-y)2,
当x=12,y=9时,
原式=9.
(2)原式=4a2-b2+2ab+b2-4a2
=2ab,
当a=-$\frac{1}{2}$,b=2时,
原式=-2.
点评 此题考查整式的化简求值,先利用整式的乘法计算公式和计算方法计算合并,进一步代入求得答案即可.

练习册系列答案
相关题目
9.甲市欲将一批水果运往乙市销售,现有火车、汽车两种运输方式,这两种运输方式的所需费用如下表(途中费用是指每公里所需的运输费用):
设甲、乙两市间的距离为xkm,
(1)如果用y1,y2分别表示使用火车、汽车运输时的总支出费用,分别写出y1,y2与x间的表达式;
(2)当x=300时,应采用哪种运输方式,才能使运输时的总支出费用最小?
| 运输工具 | 途中费用(元/km) | 装卸总费用(元) |
| 火车 | 4 | 2000 |
| 汽车 | 8 | 1000 |
(1)如果用y1,y2分别表示使用火车、汽车运输时的总支出费用,分别写出y1,y2与x间的表达式;
(2)当x=300时,应采用哪种运输方式,才能使运输时的总支出费用最小?
6.如果函数y=x-b与y=-2x+4的图象的交点坐标是(2,0),那么二元一次方程组$\left\{\begin{array}{l}{x-y=b}\\{2x+y=4}\end{array}\right.$的解是( )
| A. | (2,0) | B. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | D. | 以上答案都不对 |
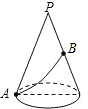 如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?
如图,一个圆锥的母线长为10cm,底面半径为5cm,在圆锥的底面边缘上一点A处有一只蚂蚁,想吃到点A相对的母线的中点B处的一粒砂糖,这只蚂蚁从点A出发,沿着曲面爬到点B,最短路线的长是多少?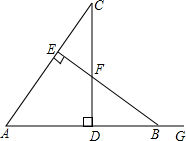 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.