题目内容
18．
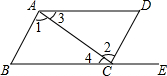如图，给出下列条件：其中，能推出AB∥DC的是（ ）①∠1=∠2； ②∠3=∠4；
③∠B=∠DCE； ④AD∥BC且∠B=∠D．
| A． | ①④ | B． | ②③ | C． | ①③ | D． | ①③④ |
分析 根据平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行分别进行分析即可．
解答 解：①∵∠1=∠2，
∴AB∥CD，
②∵∠3=∠4，
∴AD∥BC；
③∵∠B=∠DCE，
∴AB∥CD；
④∵AD∥BC，
∴∠D=∠DCE，
∵∠B=∠D，
∴∠B=∠DCE，
∴AB∥CD；
能推出AB∥DC的是①③④，
故选：D．
点评 此题主要考查了平行线的判定定理，关键是掌握平行线的判定方法．
练习册系列答案
相关题目
9．甲市欲将一批水果运往乙市销售，现有火车、汽车两种运输方式，这两种运输方式的所需费用如下表（途中费用是指每公里所需的运输费用）：
设甲、乙两市间的距离为xkm，
（1）如果用y1，y2分别表示使用火车、汽车运输时的总支出费用，分别写出y1，y2与x间的表达式；
（2）当x=300时，应采用哪种运输方式，才能使运输时的总支出费用最小？
| 运输工具 | 途中费用（元/km） | 装卸总费用（元） |
| 火车 | 4 | 2000 |
| 汽车 | 8 | 1000 |
（1）如果用y1，y2分别表示使用火车、汽车运输时的总支出费用，分别写出y1，y2与x间的表达式；
（2）当x=300时，应采用哪种运输方式，才能使运输时的总支出费用最小？
6．如果函数y=x-b与y=-2x+4的图象的交点坐标是（2，0），那么二元一次方程组$\left\{\begin{array}{l}{x-y=b}\\{2x+y=4}\end{array}\right.$的解是（ ）
| A． | （2，0） | B． | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | D． | 以上答案都不对 |
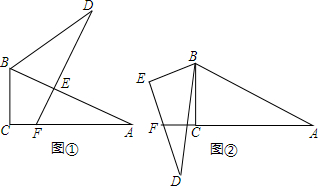
如图，在第1个△ABA1中，∠B=20°，∠BAA1=∠BA1A，在A1B上取一点C，延长AA1到A2，使得在第2个△A1CA2中，∠A1CA2=∠A1A2C；在A2C上取一点D，延长A1A2到A3，使得在第3个△A2DA3中，∠A2DA3=∠A2A3D；…，按此做法进行下去，第三个三角形中，以A3为顶点的底角的度数为20°；第n个三角形中以An为顶点的底角的度数为$\frac{80°}{{2}^{n-1}}$．