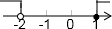题目内容
2.二元一次方程组$\left\{\begin{array}{l}{3x+2y=10}\\{kx+(k+2)y=6}\end{array}\right.$的解x,y的值相等,则k的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{5}{2}$ |
分析 把x=y代入第一个方程可求得x、y的值,再把x、y的值代入第二个方程可求得k的值.
解答 解:
∵二元一次方程组$\left\{\begin{array}{l}{3x+2y=10}\\{kx+(k+2)y=6}\end{array}\right.$的解x,y的值相等,
∴把x=y代入3x+2y=10,可得3x+2x=10,解得x=y=2,
把x=y=2代入方程kx+(k+2)y=6,可得2k+2(k+2)=6,解得k=$\frac{1}{2}$,
故选A.
点评 本题主要考查方程组的解的概念,掌握方程组的解满足方程组的每一个方程是解题的关键.

练习册系列答案
相关题目
17.如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形填写下表:
(2)写出链条的总长度y(cm)与节数n的函数关系;
(3)如果一辆22型的自行车由50节链条环形链接而成,那么这辆自行车的链条链接后的总长度.

(1)观察图形填写下表:
| 链条节数(n) | 2 | 3 | 4 |
| 链条总长度y(cm) | 4.2 | 5.9 | 7.6 |
(3)如果一辆22型的自行车由50节链条环形链接而成,那么这辆自行车的链条链接后的总长度.

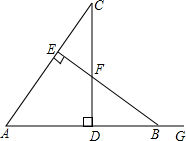 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
 如图,在四边形ABCD中,∠B=∠C=60°,BC=1,以CD为直径作圆与AB相切于点M,且交BC边于E点,求BE的长.
如图,在四边形ABCD中,∠B=∠C=60°,BC=1,以CD为直径作圆与AB相切于点M,且交BC边于E点,求BE的长.