题目内容
6.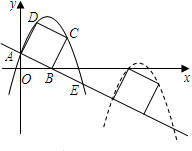 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.(1)求抛物线的解析式;
(2)若矩形以每秒$\sqrt{5}$个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设矩形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
(3)在(2)的条件下,抛物线与矩形一起平移,同时D落在x轴上时停止,求抛物线上C,E两点间的抛物线弧所扫过的面积.
分析 (1)可先根据AB所在直线的解析式求出A,B两点的坐标,即可得出OA、OB的长.过D作DH⊥y轴于H,则△ADH∽△BAO,由此可得出DH、AH的长,也就能求出D的坐标,同理可求出C的坐标;可根据A、C、D三点的坐标,用待定系数法求出抛物线的解析式;
(2)要分三种情况进行讨论:
①当F点在A′B′之间时,即当0<t≤1时,此时S为三角形FBG的面积,可用正方形的速度求出AB′的长,即可求出B′F的长,然后根据∠GFB′的正切值求出B′G的长,即可得出关于S、t的函数关系式.
②当D′逐渐移动到x轴的过程中,即当1<t≤3时,此时S为五边形A′B′C′HG的面积,S=正方形A′B′C′D′的面积-三角形GHD′的面积.可据此来列关于S,t的函数关系式;
(3)CE扫过的图形是个平行四边形,经过关系不难发现这个平行四边形的面积实际上就是矩形BCD′A′的面积.可通过求矩形的面积来求出CE扫过的面积.
解答 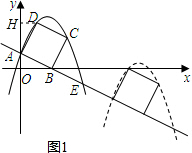 解:(1)∵直线y=-2x+2交坐标轴于A,B两点,
解:(1)∵直线y=-2x+2交坐标轴于A,B两点,
∴A(0,2),B(1,0),
如图1,过点D作DH⊥y轴于点H,
∵∠AHD=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵四边形ABCD是矩形,
∴∠DAB=90°,
∴∠DAH+∠OAB=90°,
∴∠DAH=∠ABO,
∴△DAH∽△ABO,
∴DH:AO=AH:OB=AD:AB,
∵AB:AD=1:2,
∴AH=2,DH=4,
∴OH=OA+AH=4,
∴点D(4,4),
∴C(5,2),
设抛物线为y=ax2+bx+c(a≠0),
∵抛物线过(0,2)(5,2)(4,4),
则$\left\{\begin{array}{l}{c=2}\\{25a+5b+c=0}\\{16a+4b+c=0}\end{array}\right.$,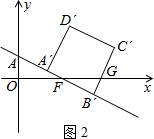 解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{5}{2}}\\{c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{5}{2}}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为:$y=-\frac{1}{2}{x^2}+\frac{5}{2}x+2$;
(2)①∵当点A运动到x轴上时,t=1,
∴当0<t≤1时,如图2,
∵∠OFA=∠GFB′,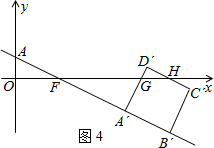 tan∠OFA=$\frac{OA}{OF}$=2,
tan∠OFA=$\frac{OA}{OF}$=2,
∴tan∠GFB′=$\frac{GB′}{FB′}$=2,
∴GB′=2$\sqrt{5}$t
∴S△FB′G=$\frac{1}{2}$FB′×GB′=$\frac{1}{2}$×$\sqrt{5}$t×2$\sqrt{5}$=5t2;
②当点D运动到x轴上时,t=3,
当1<t≤3时,如图4,
∵A′G=2$\sqrt{5}$t-2$\sqrt{5}$,
∴GD′=2$\sqrt{5}$-(2$\sqrt{5}$t-2$\sqrt{5}$)=4$\sqrt{5}$-2$\sqrt{5}$t,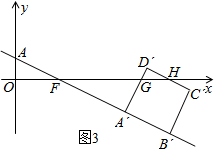
∵S△AOF=$\frac{1}{2}$×1×2=1,OA=2,△AOF∽△GD′H
∴$\frac{{S}_{△AOF}}{{S}_{△GD′H}}$=($\frac{OA}{DG′}$)2,
∴S△GD′H=5t2-20t+20,
∵S矩形=2$\sqrt{5}$×$\sqrt{5}$=10,
∴S=10-(5t2-20t+20)=-5t2+20t-10;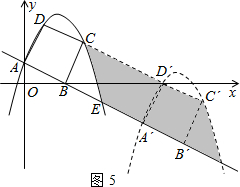 (3)如图5,∵D落在x轴上,
(3)如图5,∵D落在x轴上,
∴t=3,
∴BB′=AA′=3$\sqrt{5}$,
∵AD=2$\sqrt{5}$,
∴由平移的性质可得:S阴影=S矩形BB′C′C=S矩形AA′D′D=AD×AA′=2$\sqrt{5}$×3$\sqrt{5}$=30.
点评 此题属于二次函数的综合题,着重考查了待定系数法求二次函数解析式、图形平移变换、三角形相似等重要知识点,注意(2)小题中要根据正方形的不同位置分类进行讨论,不要漏解.

 智慧小复习系列答案
智慧小复习系列答案| A. | $\sqrt{2}$ | B. | ±$\sqrt{2}$ | C. | $\root{3}{2}$ | D. | -$\root{3}{2}$ |
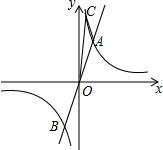 如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.
如图,已知直线y=3x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为2.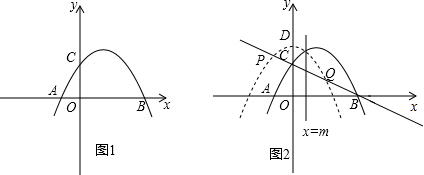
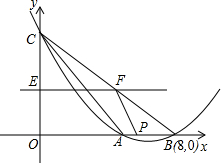 如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.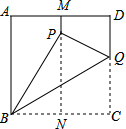 如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.
如图,有一张面积为3的正方形纸片ABCD,M,N分别是AD,BC边的中点,将C点折叠至MN上,落在P点的位置,折痕为BQ,连结PQ,则PQ=1.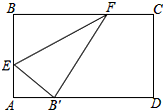 如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.