题目内容
10.若$\frac{A}{x+2}$+$\frac{B}{x-3}$=$\frac{7x-11}{{x}^{2}-x-6}$,求A、B的值.分析 首先把左边异分母分式通分,再根据同分母分式加法的运算方法求和,然后根据等式两边的分子相同,列出二元一次方程,解方程组,求出A、B的值是多少即可.
解答 解:$\frac{A}{x+2}$+$\frac{B}{x-3}$
=$\frac{A(x-3)}{{x}^{2}-x-6}+\frac{B(x+2)}{{x}^{2}-x-6}$
=$\frac{(A+B)x+2B-3A}{{x}^{2}-x-6}$
=$\frac{7x-11}{{x}^{2}-x-6}$
所以$\left\{\begin{array}{l}{A+B=7}\\{2B-3A=-11}\end{array}\right.$,
解得$\left\{\begin{array}{l}{A=5}\\{B=2}\end{array}\right.$.
点评 (1)此题主要考查了分式的加减法的运算方法,解答此题的关键是要熟练掌握通分的方法,把异分母分式的加减法转化为同分母分式的加减法.
(2)此题还考查了二元一次方程的求解,要熟练掌握二元一次方程组的求解方法.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
20.如果分式$\frac{2}{x-3}$无意义,那么x的取值范围为( )
| A. | x>3 | B. | x≥3 | C. | x=3 | D. | x≠3 |
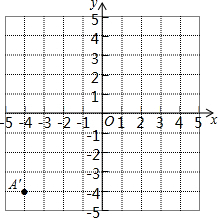 已知在平面直角坐标系中有三点A(1,2)、B(4,3)、C(3,1),请回答如下问题:
已知在平面直角坐标系中有三点A(1,2)、B(4,3)、C(3,1),请回答如下问题: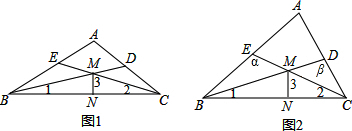
 如图所示,直线AB与x轴交于A(1,0),与y轴交于B(0,-2).
如图所示,直线AB与x轴交于A(1,0),与y轴交于B(0,-2).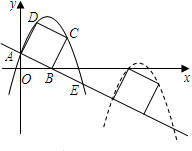 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.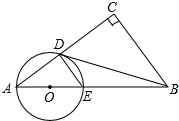 已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A.
已知:如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接DE、DB,若∠CBD=∠A. 如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.
如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.