题目内容
5．计算：（1）$\frac{1}{a（a+1）}$+$\frac{1}{（a+1）（a+2）}$+…+$\frac{1}{（a+2006）（a+2007）}$；
（2）$\frac{2}{1-2x}$+$\frac{2}{1+2x}$+$\frac{4}{1+4{x}^{2}}$+$\frac{8}{1+16{x}^{4}}$．
分析 （1）原式利用拆项法变形，抵消合并即可得到结果；
（2）原式两项两项结合，通分并利用同分母分式加法法则计算即可得到结果．
解答 解：（1）原式=$\frac{1}{a}$-$\frac{1}{a+1}$+$\frac{1}{a+1}$-$\frac{1}{a+2}$+…+$\frac{1}{a+2006}$-$\frac{1}{a+2007}$=$\frac{1}{a}$-$\frac{1}{a+2007}$=$\frac{2007}{a（a+2007）}$；
（2）原式=$\frac{2+4x+2-4x}{1-4{x}^{2}}$+$\frac{4}{1+4{x}^{2}}$+$\frac{8}{1+16{x}^{4}}$=$\frac{8}{1-16{x}^{4}}$+$\frac{8}{1+16{x}^{4}}$=$\frac{16}{1-256{x}^{8}}$．
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．若一次函数y=（2-3m）x-4的图象经过点A（x1，y1）和点B（x2，y2），当x1＜x2时，y1＞y2，则m的取值范围是（ ）
| A． | m＜$\frac{3}{2}$ | B． | m$＞\frac{3}{2}$ | C． | m$＜\frac{2}{3}$ | D． | m$＞\frac{2}{3}$ |
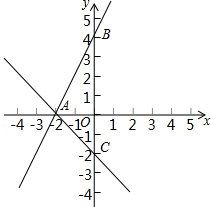如图，已知一次函数y=2x+a与y=-x+b的图象都经过点A（-2，0）且与y轴分别交于B，C两点．
已知，FA，DF分别平分∠EAC，∠CDB，试探索∠C，∠F，∠B之间的关系．