题目内容
10.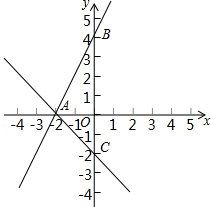 如图,已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0)且与y轴分别交于B,C两点.
如图,已知一次函数y=2x+a与y=-x+b的图象都经过点A(-2,0)且与y轴分别交于B,C两点.(1)分别求出这两个一次函数的解析式;
(2)求△ABC的面积.
分析 (1)把A点坐标分别代入两函数解析式,可求得a、b的值,可求得两函数的解析式;
(2)由两函数解析式,可求得B、C两点的坐标,可求得△ABC的面积.
解答 解:(1)把A(-2,0)分别代入y=2x+a和y=-x+b得,a=4,b=-2,
∴这两个函数分别为y=2x+4和y=-x-2;
(2)在y=2x+4和y=-x-2中,
令x=0,可分别求得y=4和y=-2,
∴B(0,4),C(0,-2),
又∵A(-2,0),
∴OA=2,BC=6,
∴S△ABC=$\frac{1}{2}$OA•BC=$\frac{1}{2}$×2×6=6.
点评 本题主要考查待定系数法求函数解析式,掌握函数图象的交点坐标满足每个函数的解析式是解题的关键.

练习册系列答案
相关题目
20.已知一次函数y=kx+b的函数值y随x的增大而增大,且其图象与y轴的负半轴相交,则对k和b的符号判断正确的是( )
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |