题目内容
14.若菱形周长等于高的$\frac{8\sqrt{3}}{3}$倍,则菱形的四个内角为120°,120°,60°,60°.分析 根据菱形四条边相等的性质,构造直角三角形DEC,从而利用30°角所对直角边等于斜边一半可求出∠DCE,进而可得出答案.
解答 解:设菱形的边长为a,高为h,
则依题意,4a=$\frac{8\sqrt{3}}{3}$h,即$\frac{h}{a}$=$\frac{\sqrt{3}}{2}$,
过点D作BC边上的高,与BC的延长线交于点E,
∵sin∠DCE=$\frac{DE}{CD}$=$\frac{h}{a}$=$\frac{\sqrt{3}}{2}$,
∴∠DCE=60°
∴∠BCD=∠BAD=120°,
∴∠ABC=∠ADC=60°
故答案为120°,120°,60°,60°.
点评 此题考查菱形的知识,熟悉菱形的性质,及一些特殊的直角是解题的关键,画出图形再解题有助于理清思路.

练习册系列答案
相关题目
 如图,⊙O的半径为R,点A,B,C,D在⊙O上,且AB=BC=CD=R,求证:
如图,⊙O的半径为R,点A,B,C,D在⊙O上,且AB=BC=CD=R,求证: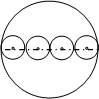 如图,5个圆的圆心在同一条直线上,且互相相切,若大圆直径是12,4个小圆大小相等,则这5个圆的周长的和为24π.
如图,5个圆的圆心在同一条直线上,且互相相切,若大圆直径是12,4个小圆大小相等,则这5个圆的周长的和为24π.