题目内容
12.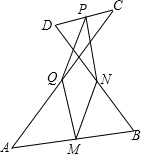 如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.
如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.
分析 连接AD、BC,如图,只需运用三角形中位线定理就可证到四边形MNPQ的两组对边分别相等,根据平行四边形的判定即可解决问题.
解答 证明:连接AD、BC,如图.
∵M、N、P、Q分别是线段AB、BD、CD、AC的中点,
∴PQ=MN=$\frac{1}{2}$AD,QM=PN=$\frac{1}{2}$BC,
∴四边形MNPQ是平行四边形.
点评 本题主要考查了三角形中位线定理、平行四边形的判定等知识,由多中点联想到三角形中位线定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.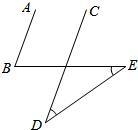 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
 如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )
如图,AB∥CD,∠D=∠E=30°,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
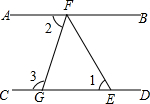 如图,直线AB∥CD,点F在直线AB上,点G、E在直线CD上,FE平分∠BFG,且∠1=50°,求∠2与∠3的度数.
如图,直线AB∥CD,点F在直线AB上,点G、E在直线CD上,FE平分∠BFG,且∠1=50°,求∠2与∠3的度数.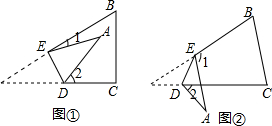

 如图,已知ED∥AC,∠EDF=∠A,∠FDC=30°.求∠B的度数.
如图,已知ED∥AC,∠EDF=∠A,∠FDC=30°.求∠B的度数.