题目内容
7.解下列不等式(组)(1)1-$\frac{2-3x}{5}$$>\frac{1+x}{2}$;
(2)$\left\{\begin{array}{l}{5x-2<3(x-2)}\\{\frac{1}{2}x-5≥1-\frac{3}{2}x}\end{array}\right.$.
分析 (1)去分母、去括号、移项、合并同类项、系数化成1即可求解;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答 解:(1)去分母,得10-2(2-3x)>5(1+x),
去括号,得10-2+6x>5+5x,
移项,得6x-5x>5-10+2,
合并同类项,得x>-3;
(2)$\left\{\begin{array}{l}{5x-2<3(x-2)…①}\\{\frac{1}{2}x-5≥1-\frac{3}{2}x…②}\end{array}\right.$,
解①得x<-2,
解②得x≥3,
则不等式组无解.
点评 本题考查了一元一次不等式组的解集:几个一元一次不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
19.某小区开展“节约用水,从我做起”活动,下表是从该小区抽取的10个家庭与上月比较的一个月的节水情况统计:
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
| 节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 家庭数(个) | 1 | 2 | 2 | 4 | 1 |
| A. | 0.42和0.4 | B. | 0.4和0.4 | C. | 0.42和0.45 | D. | 0.4和0.45 |
17.下列命题中是假命题的是( )
| A. | 一个三角形中至少有两个锐角 | |
| B. | 在同一平面内,垂直于同一直线的两条直线平行 | |
| C. | 同角的补角相等 | |
| D. | 如果a为实数,那么|a|>0 |
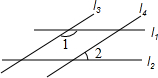 如图:直线l1∥l2,l3∥l4,∠1比∠2的3倍少20°,则∠1=130°,∠2=50°.
如图:直线l1∥l2,l3∥l4,∠1比∠2的3倍少20°,则∠1=130°,∠2=50°.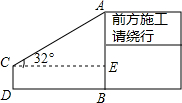 如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m) 如图,在平面直角坐标系中,?ABCD的顶点A、B、C、D的坐标分别是(-5,0),(-2,0),(-3,2).
如图,在平面直角坐标系中,?ABCD的顶点A、B、C、D的坐标分别是(-5,0),(-2,0),(-3,2).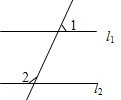 如图,若l1∥l2,∠1=44°45′,则∠2=135°15′.
如图,若l1∥l2,∠1=44°45′,则∠2=135°15′.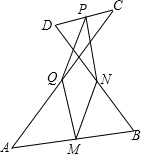 如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.
如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.