题目内容
3.把三角形纸片ABC沿DE折叠.(1)如图①,当点A落在四边形BCDE内部时,∠A、∠1、∠2有怎样的数量关系?写出这个关系式,并证明你的结论;
(2)如图②,当点A落在四边形BCDE外部时,∠A、∠1、∠2有怎样的数量关系?写出这个关系式,并证明你的结论.
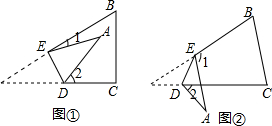
分析 (1)由对折有∠DEF=∠AED,∠EDF=∠ADE,再利用三角形的内角和、平角的定义即可求解;
(2)由对折有∠DEF=∠AED,∠EDF=∠ADE,再利用三角形内角和、平角的定义即可求解.
解答 解:(1)2∠A=∠1+∠2.
理由如下:如图①,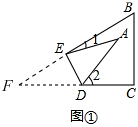
由折叠有,∠DEF=∠AED,∠EDF=∠ADE,
∵∠DEF+∠AED+∠1=180°,
∴∠1=180°-(∠DEF+∠AED)=180°-2∠AED,
∴∠AED=$\frac{180°-∠1}{2}$
同理:∠ADE=$\frac{180°-∠2}{2}$,
∵∠A+∠ADE+∠AED=180°,
∴∠A+$\frac{180°-∠2}{2}$+$\frac{180°-∠1}{2}$=180°,
∴2∠A=∠1+∠2.
(2)2∠A=∠1-∠2.
如图②,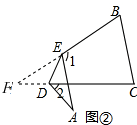
由(1)有:∠AED=$\frac{180°-∠1}{2}$,∠EDF=∠ADE,
∵∠EDF+∠EDC=180°,∠EDC=∠ADE-∠2,
∴∠ADE=$\frac{180°+∠2}{2}$
∵∠A+∠AED+∠ADE=180°,
∴∠A+$\frac{180°-∠1}{2}$+$\frac{180°+∠2}{2}$=180°,
∴2∠A=∠1-∠2.
点评 此题是折叠变换.主要考查折叠的性质,和平角,三角形内角和,式子的化简是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
8.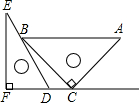 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,则∠DBC的度数为( )| A. | 25° | B. | 20° | C. | 15° | D. | 18° |
13.不等式组$\left\{\begin{array}{l}{x>4}\\{x>m}\end{array}\right.$的解集是x>4,那么m的取值范围是( )
| A. | m≥4 | B. | m≤4 | C. | 3≤x<4 | D. | 3<x≤4 |
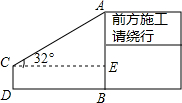 如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m) 如图,在平面直角坐标系中,?ABCD的顶点A、B、C、D的坐标分别是(-5,0),(-2,0),(-3,2).
如图,在平面直角坐标系中,?ABCD的顶点A、B、C、D的坐标分别是(-5,0),(-2,0),(-3,2).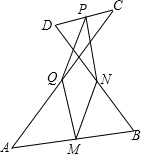 如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.
如图,已知M、N、P、Q分别是线段AB、BD、CD、AC的中点,求证:四边形MNPQ是平行四边形.