题目内容
10.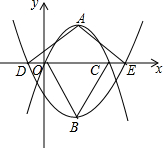 如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
分析 因为两条抛物线对称轴均为直线x=2,开口向下的抛物线过原点O,所以C点坐标为(4,0),开口向上的抛物线过D(-1,0),所以E点坐标为(5,0),所以可得OC=4,DE=6,由题意又可得△ADE的高为2,△OBC的高为3,所以△ADE与△BOC的面积比为1:1.
解答 解:依题意得:A点坐标为(2,2),B点坐标为(2,-3),
又因为顶点为A的抛物线与x轴交于O、C,所以C点坐标为(4,0),
顶点为B的抛物线与x轴交于D、E,且D(-1,0),所以E点坐标为(5,0),
所以OC=4,DE=6,
所以S△ADE=$\frac{1}{2}$×6×2=6,S△BOC=$\frac{1}{2}$×4×3=6,
所以两个三角形面积比为1:1.
故答案为:1:1.
点评 本题主要考查了抛物线的对称性,关键是由解析式确定顶点坐标及对称轴,然后再由与x轴的一个交点确定另一个交点坐标.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.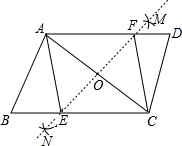 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
 如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )
如图,在?ABCD中,分别以A,C为圆心,大于$\frac{1}{2}$AC长为半径画弧,相交于点M,N,直线MN与BC,AD分别相交于点E,F,则在四边形AECF中一定有( )| A. | AE=AF | B. | AC=EF | C. | ∠EAF=90° | D. | ∠AFE=45° |
2.使不等式x-2≥-3与2x+3<5同时成立的x的整数值是( )
| A. | -2,-1,0 | B. | 0,1 | C. | -1,0 | D. | 不存在 |
20.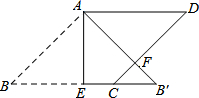 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2$-\sqrt{2}$ | D. | 2$\sqrt{2}$-2 |
 如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.
如图,平行四边形ABCD的周长为60厘米,BF,DE分别为高,DC的长为18厘米.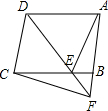 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证: