题目内容
1.从平行四边形的一个锐角的顶点作不过该顶点的两边上的两条高线,如果这两条高线的夹角是135°,则这个平行四边形的锐角的度数是45°.分析 根据四边形内角和定理即可解决问题.
解答 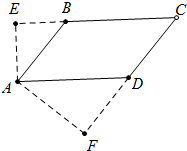 解:如图,四边形ABCD是平行四边形,∠BAD是锐角,AE⊥CB,AF⊥CD,垂足分别为E、F.
解:如图,四边形ABCD是平行四边形,∠BAD是锐角,AE⊥CB,AF⊥CD,垂足分别为E、F.
∵∠EAF=135°,∠EAF+∠E+∠F+∠C=360°,
∴∠C=45°.
∴这个平行四边形的锐角的度数是45°.
故答案为45°.
点评 本题考查平行四边形的性质、四边形内角和定理等知识,解题的关键是四边形内角和定理的运用,属于中考常考题型.

练习册系列答案
相关题目
16.反比例函数y=$\frac{k}{x}$,当自变量x的值从1增加到2,函数值就减少了3,则函数解析式为( )
| A. | y=$\frac{3}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{6}{x}$ | D. | y=3x |
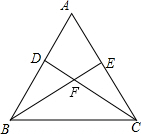 在△ABC中,AB=AC,D,E分别在边AB,AC上,AD=AE,DC,BE交于点F,求证:△BDC≌△CEB.
在△ABC中,AB=AC,D,E分别在边AB,AC上,AD=AE,DC,BE交于点F,求证:△BDC≌△CEB.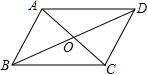 如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.
如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.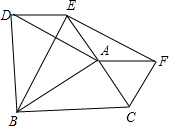 如图,分别以△ABC的三边向外作等边三角形:△ABD,△BCE,△ACF,连接DE,EF.
如图,分别以△ABC的三边向外作等边三角形:△ABD,△BCE,△ACF,连接DE,EF.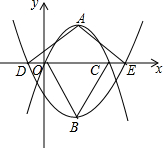 如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.