题目内容
15.化简求值:已知M=$\frac{1+2n+{n}^{2}}{1-{n}^{2}}$-$\frac{n}{n-1}$.(1)化简M;
(2)当n满足不等式组$\left\{\begin{array}{l}{1-n≤0}\\{n-3<0}\end{array}\right.$ 且n为整数时,求M的值.
分析 (1)先通分,再把分子相加减,把结果化为最简分式即可;
(2)先求出n的取值范围,再得出n的整数值代入(1)中M的表达式即可.
解答 解:(1)M=$\frac{(1+n)^{2}}{(1+n)(1-n)}$+$\frac{n(1+n)}{(1+n)(1-n)}$
=$\frac{{(1+n)}^{2}+n(1+n)}{(1+n)(1-n)}$
=$\frac{(1+n)(1+2n)}{(1+n)(1-n)}$
=$\frac{1+2n}{1-n}$;
(2)解不等式组$\left\{\begin{array}{l}1-n≤0\\ n-3<0\end{array}\right.$得,1≤n<3,
故n的整数解为1,2,
当n=1时原式无意义;
当n=2时,原式=$\frac{1+4}{1-2}$=-5.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
5.给出的下列各数:-1,0,0.5,$\sqrt{7}$,$\root{3}{8}$,π,其中是无理数的个数有( )
| A. | 0个 | B. | 2个 | C. | 3个 | D. | 6个 |
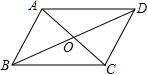 如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.
如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.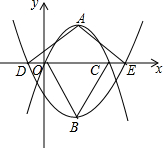 如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.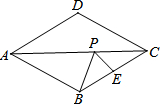 如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.
如图,在菱形ABCD中,AD=6,∠ABC=120°,E是BC的中点,P为对角线AC上的一个动点,则PE+PB的最小值为3$\sqrt{3}$.