题目内容
20.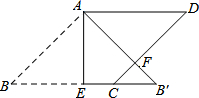 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2$-\sqrt{2}$ | D. | 2$\sqrt{2}$-2 |
分析 由在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,可求得AE的长,由折叠易得△ABB′为等腰直角三角形,得到CB′=2BE-BC=2$\sqrt{2}$-2,根据平行线的性质得到∠FCB′=∠B=45°,又由折叠的性质得到∠B′=∠B=45°,即可得到结论.
解答 解:∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=$\sqrt{2}$,由折叠易得△ABB′为等腰直角三角形,
∴S△ABB′=$\frac{1}{2}$BA•AB′=2,S△ABE=1,
∴CB′=2BE-BC=2$\sqrt{2}$-2,
∵AB∥CD,
∴∠FCB′=∠B=45°,
又由折叠的性质知,∠B′=∠B=45°,
∴CF=FB′=2-$\sqrt{2}$.
故选C.
点评 此题考查了菱形的性质以及等腰直角三角形的性质,折叠的性质,此题难度不大.

练习册系列答案
相关题目
5.给出的下列各数:-1,0,0.5,$\sqrt{7}$,$\root{3}{8}$,π,其中是无理数的个数有( )
| A. | 0个 | B. | 2个 | C. | 3个 | D. | 6个 |
12.若线段AB的端点坐标分别为A(-2,3),B(0,5),将它向下平移5个单位,则其端点坐标变为( )
| A. | A′(3,3),B′(0,0) | B. | A′(-2,-2),B′(0,0) | C. | A′(3,3),B′(5,5) | D. | A′(3,3),B′(-5,5) |
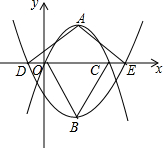 如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.
如图,在平面直角坐标系中,顶点为A的抛物线y=a1(x-2)2+2与x轴交于点O、C.顶点为B的抛物线y=a2(x-2)2-3与x轴交于点D、E.若点D的坐标为(-1,0),则△ADE与△BOC的面积比为1:1.