题目内容
 如图,A、B两点的坐标分别是(1,
如图,A、B两点的坐标分别是(1,| 3 |
| 2 |
| 3 |
| 2 |
(1)求△ABC的面积;
(2)在图中将△ABC作关于y轴对称的图形,再向下平移
| 3 |
| 2 |
(3)求△A′B′C′的面积.
考点:作图-轴对称变换,作图-平移变换
专题:
分析:(1)先求出AB的长,再求出AB边上的高,根据三角形的面积公式即可得出结论;
(2)根据题意画出图形,写出A′,B′,C′的坐标即可;
(3)根据图形平移不变性的性质可直接得出结论.
(2)根据题意画出图形,写出A′,B′,C′的坐标即可;
(3)根据图形平移不变性的性质可直接得出结论.
解答: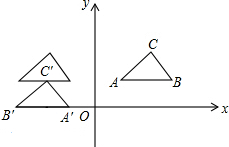 解:(1)∵A、B两点的坐标分别是(1,
解:(1)∵A、B两点的坐标分别是(1,
),(4,
),点C的坐标是(3,3),
∴AB=4-1=3,AB边上的高=3-
=
,
∴S△ABC=
×3×
=
;
(2)如图所示,
A′(-1,0),B′(-4,0),C′(-3,
);
(3)∵△ABC与△A′B′C′的大小与形状完全相同,
∴S△A′B′C′=S△ABC=
.
 解:(1)∵A、B两点的坐标分别是(1,
解:(1)∵A、B两点的坐标分别是(1,| 3 |
| 2 |
| 3 |
| 2 |
∴AB=4-1=3,AB边上的高=3-
| 3 |
| 2 |
| 3 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
(2)如图所示,
A′(-1,0),B′(-4,0),C′(-3,
| 3 |
| 2 |
(3)∵△ABC与△A′B′C′的大小与形状完全相同,
∴S△A′B′C′=S△ABC=
| 9 |
| 4 |
点评:本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
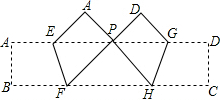 如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( )
如图所示,折叠矩形纸条ABCD,使B,C两点落在AD边的P点处,折痕为EF,GH,若∠FPH的度数恰好为90°,PF=8,PH=6,则矩形ABCD的边BC的长为( )| A、20 | B、22 | C、24 | D、30 |
 如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )①BE=CF ②AE是∠DAB的角平分线 ③∠DAE+∠DCF=120°.
| A、① | B、①② |
| C、①②③ | D、都不正确 |
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点.
如图,△ABC中,BD平分∠ABC,AD⊥BD,D为垂足,E为AC的中点. 市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,且DE=5cm,求BC的长.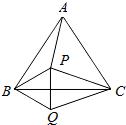 如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图所示,点P是等边三角形ABC内的一点,连接PA、PB、PC以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.