题目内容
武汉市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销,经过调查得到如下数据:
(1)猜想y与x的函数关系,并求出函数关系;
(2)当销售单价为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价);
(3)武汉市物价部门规定,该工艺品销售单价最高不能超过35元/件,若此工艺厂要求该产品利润最低为5000元,那么销售单价的范围为多少?
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价);
(3)武汉市物价部门规定,该工艺品销售单价最高不能超过35元/件,若此工艺厂要求该产品利润最低为5000元,那么销售单价的范围为多少?
考点:二次函数的应用
专题:
分析:(1)设y与x的函数关系式为y=kx+b,由待定系数法求出其解即可;
(2)设工艺厂试销该工艺品每天获得的利润为W元,根据利润=销售总价-成本总价表示出W与x的数量关系,由二次函数的性质就可以求出结论;
(3)由(2)的解析式建立不等式,求出其解即可.
(2)设工艺厂试销该工艺品每天获得的利润为W元,根据利润=销售总价-成本总价表示出W与x的数量关系,由二次函数的性质就可以求出结论;
(3)由(2)的解析式建立不等式,求出其解即可.
解答:解:(1)设y与x的函数关系式为y=kx+b,由题意,得:
解得:
.
故y与x的函数关系式为y=-10x+700;
(2)设工艺厂试销该工艺品每天获得的利润为W元,由题意,得
W=(-10x+700)(x-10),
W=-10(x-40)2+9000,
∵a=-10<0,
∴x=40时,W最大=9000元.
答:销售单价定为40时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元;
(3)由题意,得
-10(x-40)2+9000≥5000,
(x-20)(x-60)≤0,则
①或
②
解得:①无解;
②20≤x≤60.
∵x≤35,
∴20≤x≤35.
答:销售单价20≤x≤35时,工艺厂试销该工艺品每天获得的利润不低于5000元.
|
解得:
|
故y与x的函数关系式为y=-10x+700;
(2)设工艺厂试销该工艺品每天获得的利润为W元,由题意,得
W=(-10x+700)(x-10),
W=-10(x-40)2+9000,
∵a=-10<0,
∴x=40时,W最大=9000元.
答:销售单价定为40时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元;
(3)由题意,得
-10(x-40)2+9000≥5000,
(x-20)(x-60)≤0,则
|
|
解得:①无解;
②20≤x≤60.
∵x≤35,
∴20≤x≤35.
答:销售单价20≤x≤35时,工艺厂试销该工艺品每天获得的利润不低于5000元.
点评:本题考查了待定系数法求一次函数的解析式的运用,由利润率问题的数量关系求二次函数的解析式的运用,一元二次不等式的解法的运用,解答时求出函数的解析式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
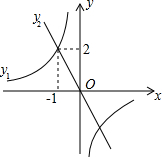 如图,直线y1=k1x与双曲线y2=
如图,直线y1=k1x与双曲线y2=| k2 |
| x |
| A、x<-1 |
| B、0<x<1 |
| C、x<-1或0<x<1 |
| D、-1<x<0或x>1 |
 如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )A、4
| ||
| B、8 | ||
C、4
| ||
| D、9 |
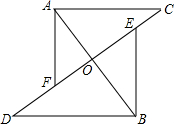 如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.
如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.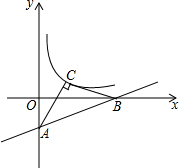 已知:如图,直线y=
已知:如图,直线y= 如图,A、B两点的坐标分别是
如图,A、B两点的坐标分别是 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD= 先作图,再证明.
先作图,再证明.