题目内容
 如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )
如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正弦值等于( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:圆周角定理,锐角三角函数的定义
专题:网格型
分析:首先根据圆周角定理可知,∠AED=∠ACB,在Rt△ACB中,根据锐角三角函数的定义求出∠AED的正弦值.
解答:解:∵∠AED和∠ABC所对的弧长都是
,
∴∠AED=∠ABC.
∴在Rt△ACB中,sin∠ABC=
,
∵AC=1,AB=2,
∴BC=
,
∴sin∠ABC=
,
∴∠AED的正弦值等于
,
故选A.
 |
| AD |
∴∠AED=∠ABC.
∴在Rt△ACB中,sin∠ABC=
| AC |
| BC |
∵AC=1,AB=2,
∴BC=
| 5 |
∴sin∠ABC=
| ||
| 5 |
∴∠AED的正弦值等于
| ||
| 5 |
故选A.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解答此题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
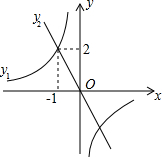 如图,直线y1=k1x与双曲线y2=
如图,直线y1=k1x与双曲线y2=| k2 |
| x |
| A、x<-1 |
| B、0<x<1 |
| C、x<-1或0<x<1 |
| D、-1<x<0或x>1 |
 如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=45°,AB=8,则⊙O的半径为( )A、4
| ||
| B、8 | ||
C、4
| ||
| D、9 |
已知方程组
的解为
,则a-b的值为( )
|
|
| A、10 | ||
B、
| ||
C、-
| ||
| D、-10 |
若2a-b=3,则9-4a+2b的值为( )
| A、3 | B、6 | C、12 | D、0 |
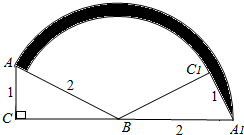 如图所示,△ABC中,∠ACB=90°,AC=1cm,AB=2cm,以B为中心,将△ABC顺时针旋转,使得点A落在边CB延长线上的A1点,此时点C落在点C1,则在旋转中,边AC变到A1C1所扫过的面积为
如图所示,△ABC中,∠ACB=90°,AC=1cm,AB=2cm,以B为中心,将△ABC顺时针旋转,使得点A落在边CB延长线上的A1点,此时点C落在点C1,则在旋转中,边AC变到A1C1所扫过的面积为 如图,A、B两点的坐标分别是
如图,A、B两点的坐标分别是 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=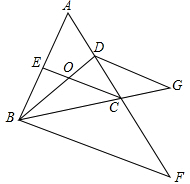 如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.
如图,△ABC中,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,BD,CE交于点O,F,G分别是AC,BC延长线上一点,且∠EOD+∠OBF=180°,∠DBC=∠G,指出图中所有平行线,并说明理由.