题目内容
 市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
市政府大力扶持节能环保产业,某企业研发出一种节能环保产品,获得市政府提供的120万元无息贷款,用于该产品的生产与销售,并约定用该产口的利润逐步偿还无息贷款,已知该产口的生产成本为每件60元,员工每人每月的工资为3000元,公司每月需支付其他费用15万元,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.(1)当60≤x≤80时,y与x之间的函数关系式是
当80<x<120时,y与x之间的函数关系式是
(2)当销售单价定为70元时,为保证公司每月利润达到6万元(利润=销售额-生产成本-员工工资-其他费用),该公司安排员工多少人?
(3)若该公司有50名员工,则该公司最快可在几个月后还清无息贷款?
考点:二次函数的应用
专题:
分析:(1)分别利用待定系数法求一次函数解析式解答;
(2)设安排a名员工,根据(1)求出定价50元时的销售件量,然后利润的表示列出方程,求解即可;
(3)根据x的取值范围分两种情况整理得到利润表达式,再根据二次函数的最值问题求出利润取得最大值时的情况,然后根据要尽早还清贷款,获得利润最大确定出单价,再根据贷款总额列出不等式,求解即可.
(2)设安排a名员工,根据(1)求出定价50元时的销售件量,然后利润的表示列出方程,求解即可;
(3)根据x的取值范围分两种情况整理得到利润表达式,再根据二次函数的最值问题求出利润取得最大值时的情况,然后根据要尽早还清贷款,获得利润最大确定出单价,再根据贷款总额列出不等式,求解即可.
解答:解:(1)①60≤x≤80时,设y=kx+b,
则
,
解得
,
所以,y=-0.1x+10,
②x>60时,设y=mx+n,
则
,
解得
,
所以,y=-0.05x+6;
故答案为:y=-0.1x+10,y=-0.05x+6;
(2)设安排a名员工,当单价定为70元时,销售量y=-0.1×70+10=3(万件),
(70-60)×3-15-0.25a=6,
解得a=36,
答:该公司可安排员工36人;
(3)当60≤x≤80时,利润W=(x-60)×(-0.1x+10)-15-20=-0.1(x-80)2+5,
所以,x=80时,W最大值=5(万元);
当60<x<100时,利润W=(x-70)×(-0.05x+6)-15-20=-0.05(x-95)2+10,
所以,x=95时,W最大值=10(万元),
∴要尽早还清贷款,只有当单价x=95元时,获得最大月利润10万,
设该公司n个月后还清贷款,则10n≥120,
解得n≥12,
∴该公司最少需要12个月才能完成任务.
则
|
解得
|
所以,y=-0.1x+10,
②x>60时,设y=mx+n,
则
|
解得
|
所以,y=-0.05x+6;
故答案为:y=-0.1x+10,y=-0.05x+6;
(2)设安排a名员工,当单价定为70元时,销售量y=-0.1×70+10=3(万件),
(70-60)×3-15-0.25a=6,
解得a=36,
答:该公司可安排员工36人;
(3)当60≤x≤80时,利润W=(x-60)×(-0.1x+10)-15-20=-0.1(x-80)2+5,
所以,x=80时,W最大值=5(万元);
当60<x<100时,利润W=(x-70)×(-0.05x+6)-15-20=-0.05(x-95)2+10,
所以,x=95时,W最大值=10(万元),
∴要尽早还清贷款,只有当单价x=95元时,获得最大月利润10万,
设该公司n个月后还清贷款,则10n≥120,
解得n≥12,
∴该公司最少需要12个月才能完成任务.
点评:本题考查了二次函数的应用,主要利用了待定系数法求一次函数解析式,二次函数的最值问题,读懂题目信息,理解利润的表示并列式整理得到利润的关系式是解题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
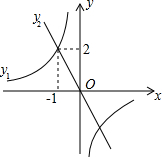 如图,直线y1=k1x与双曲线y2=
如图,直线y1=k1x与双曲线y2=| k2 |
| x |
| A、x<-1 |
| B、0<x<1 |
| C、x<-1或0<x<1 |
| D、-1<x<0或x>1 |
已知方程组
的解为
,则a-b的值为( )
|
|
| A、10 | ||
B、
| ||
C、-
| ||
| D、-10 |
在2012年全国初中数学竞赛复赛中,成都市某校9年级10名参赛学生成绩分别为:84,85,86,84,86,87,87,86,87,87,则这组数据的中位数和众数分别是( )
| A、86;87 |
| B、87;86 |
| C、86.5;87 |
| D、87;86.5 |
 如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积.
如图,已知点D是⊙O外的一点,DA为⊙O的切线,A为切点,AB为⊙O的直径,BD交⊙O于点C,若DA=4,DC=2,求图中阴影部分面积. 如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B=
如图,AB∥CD,∠B:∠O:∠D=4:3:3,则∠B= 某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m.
某工厂要赶制一批抗震救灾用的大型活动板房,如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为3.6m. 如图,A、B两点的坐标分别是
如图,A、B两点的坐标分别是