题目内容
12．在下列函数中：①y=2x-5； ②y=-3x； ③y=1-x； ④y=$\frac{1}{x}$（x＞0）．y随x的增大而减小的共有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据一次函数的性质和反比例函数的性质进行判断．
解答 解：在下列函数中：①y=2x-5； ②y=-3x； ③y=1-x； ④y=$\frac{1}{x}$（x＞0）．y随x的增大而减小的共有②③④．
故选C．
点评 本题考查了比例函数的性质：反比例函数y=$\frac{k}{x}$（k≠0）的图象是双曲线；当k＞0，双曲线的两支分别位于第一、第三象限，在每一象限内y随x的增大而减小；当k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大．也考查了一次函数的性质．
练习册系列答案
名校课堂系列答案
相关题目
2．若（a-b）•（a-b）3•（a-b）m=（a-b）11，则m的值为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
17．因为cos60°=$\frac{1}{2}$，cos240°=-$\frac{1}{2}$，所以cos240°=cos（180°+60°）=-cos60°；由此猜想、推理知：当α为锐角时有cos（180°+α）=-cosα，由此可知：cos210°=（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{2}}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | -$\sqrt{3}$ |
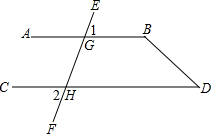如图已知∠1=∠2，∠D=50°，
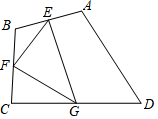如图，四边形ABCD中，点E、F、G分别为边AB、BC、CD的中点，若△EFG的面积为4，则四边形ABCD的面积为（ ）