题目内容
2.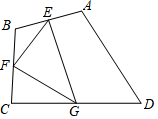 如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )| A. | 8 | B. | 12 | C. | 16 | D. | 18 |
分析 记△BEF,△DGH,△CFG,△AEH的面积分别为S1,S2,S3,S4,四边形ABCD的面积为S.连接AC.只要证明S1+S2+S3+S4=$\frac{1}{2}$S,S四边形EFGH=$\frac{1}{2}$S,即可解决问题.
解答  解:记△BEF,△DGH,△CFG,△AEH的面积分别为S1,S2,S3,S4,四边形ABCD的面积为S.连接AC.
解:记△BEF,△DGH,△CFG,△AEH的面积分别为S1,S2,S3,S4,四边形ABCD的面积为S.连接AC.
∵BF=CF,BE=AE,CG=DG,AH=DH,
∴EF∥AC,EF=$\frac{1}{2}$AC,GH∥AC,GH=$\frac{1}{2}$AC,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形,
∴S平行四边形EFGH=2S△EFG=8,
∵△BEF∽△BAC,
∴S1=$\frac{1}{4}$S△ABC,同理可得S2=$\frac{1}{4}$S△ACD,
∴S1+S2=$\frac{1}{4}$(S△ABC+S△ACD)=$\frac{1}{4}$S,
同法可得S3+S4=$\frac{1}{4}$S,
∴S1+S2+S3+S4=$\frac{1}{2}$S,
∴S四边形EFGH=$\frac{1}{2}$S,
∴S=2S四边形EFGH=16.
故选C.
点评 本题考查三角形中位线定理、平行四边形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,记住中点四边形的面积是四边形的面积的一半.

练习册系列答案
相关题目
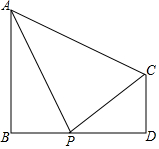 已知如图,在四边形ABDC中,AB⊥BD于B,CD⊥BD于D.P为BD上一动点(不与B、D重合),连结PA、PC,AB=9,CD=4,
已知如图,在四边形ABDC中,AB⊥BD于B,CD⊥BD于D.P为BD上一动点(不与B、D重合),连结PA、PC,AB=9,CD=4,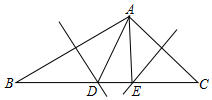 如图,在△ABC中,线段AB、AC的垂直平分线与BC的交点分别为D、E.
如图,在△ABC中,线段AB、AC的垂直平分线与BC的交点分别为D、E.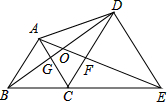 如图所示,点B、C、E在同一直线上,△ABC与△CDE都是等边三角形,则下列所有正确的结论序号为①②③⑥
如图所示,点B、C、E在同一直线上,△ABC与△CDE都是等边三角形,则下列所有正确的结论序号为①②③⑥ 已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数.
已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数.