题目内容
9. 如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )
如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )| A. | 20° | B. | 15° | C. | 10° | D. | 5° |
分析 先利用已知条件解出各段弧的角度,连接OC,求出∠EOC的角度,再利用等腰三角形的性质,解出∠E.
解答 解:如图,连接OC.
∵半径OE⊥AB,
∴$\widehat{BE}$的角度=$\frac{1}{2}$$\widehat{AB}$的角度=(180°-60°-40°)×$\frac{1}{2}$=80°,
$\widehat{BC}$的角度=80°,
∴∠EOC=160°,
∴∠E=$\frac{1}{2}$(180°-160°)=10°,
故选C.
点评 此题考查了圆周角定理以及圆心角的计算方法,以及等腰三角形中各内角的计算.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
19.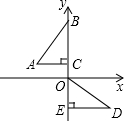 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| B. | △ABC绕点C逆时针旋转90°,再向下平移3 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C顺时针旋转90°,再向下平移3 |
 小明在学习13.2画轴对称图形这一节时,利用直尺和圆规完成了画一个点关于直线的对称点,其步骤如下:
小明在学习13.2画轴对称图形这一节时,利用直尺和圆规完成了画一个点关于直线的对称点,其步骤如下: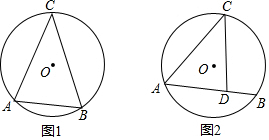
 如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.
如图,在平面直角坐标系中,二次函数y=ax2+bx+6的图象交x轴于A、B两点,交y轴于点D,点C为抛物线的顶点,且A、B两点的横坐标分别为1和3.
 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°.