题目内容
20.先化简,再求值:($\frac{x}{x+y}$+$\frac{2y}{x+y}$)•$\frac{xy}{x+2y}$÷($\frac{1}{x}$+$\frac{1}{y}$),其中x2+y2=17,(x-y)2=9.分析 先将原式进行化简,然后根据x2+y2=17,(x-y)2=9求出x+y和xy的值并代入求解即可.
解答 解:∵x2+y2=17,(x-y)2=9,
∴2xy=x2+y2-(x-y)2=17-9=8,
∴(x+y)2=x2+y2+2xy=17+8=25,
∴x+y=5,xy=4,
∴原式=$\frac{x+2y}{x+y}$×$\frac{xy}{x+2y}$÷$\frac{x+y}{xy}$
=$\frac{xy}{x+y}$×$\frac{xy}{x+y}$
=$\frac{4}{5}$×$\frac{4}{5}$
=$\frac{16}{25}$.
点评 本题考查了分式的化简求值,解答本题的关键在于先将原式进行化简,然后根据x2+y2=17,(x-y)2=9求出x+y和xy的值并代入求解.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
11.将1,2,3,4,5,6,7,8这8个数排成一行,使8的两边各数的和相等,则不同的排列方法有( )
| A. | 1152种 | B. | 576种 | C. | 288种 | D. | 144种 |
15.若x2+5x+a=(x+7)(x+b),则a+b=( )
| A. | 16 | B. | -16 | C. | 12 | D. | -12 |
9. 如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )
如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )
 如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )
如图,△ABC内接于⊙O,∠B=60°,∠A=40°,半径OE⊥AB,连接CE,则∠E等于( )| A. | 20° | B. | 15° | C. | 10° | D. | 5° |
 如图,点B是直线l上任意一点,AB⊥BC于B,且AB=BC,依语句画图并回答问题.
如图,点B是直线l上任意一点,AB⊥BC于B,且AB=BC,依语句画图并回答问题. 如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$.
如图,O是正方形ABCD的中心,M是ABCD内一点,∠DMC=90°,将△DMC绕O点旋转180°后得到△NAB,若MD=3,CM=4,则MN的长为$\sqrt{2}$. 如图,在直角三角形ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从点A出发,以4cm/s的速度在线段AB上运动;同时点Q也从点A出发,沿线段AC运动,且始终保持PQ⊥AB.以点Q为圆心,PQ为半径作⊙O.设运动时间为t(s).
如图,在直角三角形ABC中,∠ACB=90°,AC=8cm,BC=6cm.点P从点A出发,以4cm/s的速度在线段AB上运动;同时点Q也从点A出发,沿线段AC运动,且始终保持PQ⊥AB.以点Q为圆心,PQ为半径作⊙O.设运动时间为t(s).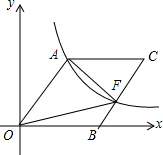 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )