题目内容
17．已知点A，B，C在⊙O上，∠C=30°，仅使用无刻度的直尺作图（保留痕迹）（1）在图①中画一个含30°的直角三角形；
（2）点D在弦AB上，在图②中画一个含30°的直角三角形．
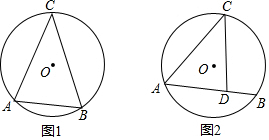
分析 （1）过点A作直径AD，连结BD，根据圆周角定理得到∠D=∠C=30°，∠ABD=90°，从而可判断△ABD满足条件；
（2）延长CD交圆于点E，过点E作直径EF，连结AF，根据圆周角定理得到∠F=∠C=30°，∠EAF=90°，从而可判断△AEF满足条件．
解答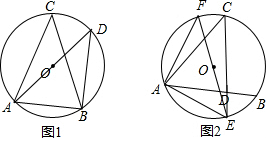 
解：（1）如图1，△ABD为所作；
（2）如图2，△AEF为所作．
点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．熟练掌握圆周角定理是解决此题的关键．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
7．
如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM=x，则x的最大值是（ ）
如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD=3，AB=5，PM=x，则x的最大值是（ ）| A． | 3 | B． | $\sqrt{5}$ | C． | 2.5 | D． | 2$\sqrt{3}$ |
如图，点B是直线l上任意一点，AB⊥BC于B，且AB=BC，依语句画图并回答问题．
如图，O是正方形ABCD的中心，M是ABCD内一点，∠DMC=90°，将△DMC绕O点旋转180°后得到△NAB，若MD=3，CM=4，则MN的长为$\sqrt{2}$．
如图，在直角三角形ABC中，∠ACB=90°，AC=8cm，BC=6cm．点P从点A出发，以4cm/s的速度在线段AB上运动；同时点Q也从点A出发，沿线段AC运动，且始终保持PQ⊥AB．以点Q为圆心，PQ为半径作⊙O．设运动时间为t（s）．
9．
如图，△ABC内接于⊙O，∠B=60°，∠A=40°，半径OE⊥AB，连接CE，则∠E等于（ ）
如图，△ABC内接于⊙O，∠B=60°，∠A=40°，半径OE⊥AB，连接CE，则∠E等于（ ）| A． | 20° | B． | 15° | C． | 10° | D． | 5° |