题目内容
10.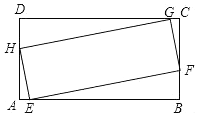 如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )
如图,四边形EFGH与四边形ABCD均为矩形,点E,F,G,H分别在边AB,BC,CD,DA上,且EF=3HE,AB=2BC,则tan∠AHE=( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{10}$ |
分析 根据四边形ABCD是矩形,四边形EFGH是矩形得到∠A=∠B=∠C=90°,∠HEF=90°,HE=GF,证得△AEH≌△CGF,于是得到CF=AH,由于△AEH∽△BEF,根据相似得出$\frac{AE}{BF}$=$\frac{AH}{BE}$=$\frac{EH}{EF}$=$\frac{1}{3}$,求出BF=3AE,CF=AH=$\frac{1}{3}$BE,根据AB=2BC求出3AE+$\frac{1}{3}$BE=$\frac{1}{2}$AB=$\frac{1}{2}$(AE+BE),求出BE=15AE,AH=5AE,即可得出答案.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
∵四边形EFGH是矩形,
∴∠HEF=90°,HE=GF,
∴∠AEH+∠BEF=∠BEF+∠BFE=90°,
∴∠AEH=∠BFE,
同理∠AEH=∠FGC,
在△AEH与△CGF中,
$\left\{\begin{array}{l}{∠A=∠C=90°}\\{∠AEH=∠CGF}\\{EH=GF}\end{array}\right.$,
∴△AEH≌△CGF,
∴CF=AH,
∵∠AEH=∠BFE,∠A=∠B,
∴△AEH∽△BEF,
∵EF=3HE,
∴$\frac{AE}{BF}$=$\frac{AH}{BE}$=$\frac{EH}{EF}$=$\frac{1}{3}$,
∴BF=3AE,CF=AH=$\frac{1}{3}$BE,
∴3AE+$\frac{1}{3}$BE=BF+CF=BC,
∵AB=2BC,
∴AE=∵AB=2BC,
∴3AE+$\frac{1}{3}$BE=$\frac{1}{2}$AB=$\frac{1}{2}$(AE+BE),
即BE=15AE,
∵$\frac{AH}{BE}$=$\frac{1}{3}$,
∴AH=5AE,
∴tan∠AHE=$\frac{AE}{AH}$=$\frac{1}{5}$,
故选A.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,矩形的性质,熟练运用定理进行推理是解题的关键.

| A. |  | B. |  | C. |  | D. |  |
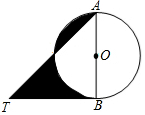 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )| A. | 2 | B. | $\frac{3}{2}$-$\frac{1}{4}$π | C. | 1 | D. | $\frac{1}{2}$+$\frac{1}{4}$π |
| A. | 3,2 | B. | 3,4 | C. | 5,2 | D. | 5,4 |
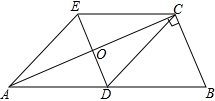 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.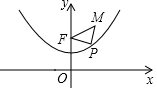 已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )
已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )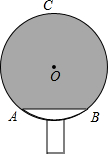 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.
如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.