题目内容
12.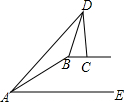 如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
分析 过点B作BG⊥AE,垂足为点G,如图.根据已知条件得到设BG=5k,则AG=12k,在Rt△BAG中,由勾股定理得,AB=13k,得到BG=15,于是得到坡顶B到AE的距离为15米.延长DC交AE于点F,根据平行线的性质得到DF⊥AE,根据矩形的性质得到AF=DF,设DC=x,则AF=36+GF,DF=x+15,得到BC=GF=x-21,根据三角函数的定义即可得到结论.
解答  解:过点B作BG⊥AE,垂足为点G,如图.
解:过点B作BG⊥AE,垂足为点G,如图.
∵i=tan∠BAG=$\frac{BG}{AG}$=5:12,
∴设BG=5k,则AG=12k,
在Rt△BAG中,由勾股定理得,AB=13k,
∴13k=39,解得k=3,
∴BG=15,
∴坡顶B到AE的距离为15米.
延长DC交AE于点F,
∵BC⊥DC,BC∥AE,
∴DF⊥AE,
∴四边形BCFG是矩形,CF=BG=15,BC=GF,
∵∠DAF=45°,
∴AF=DF,
设DC=x,则AF=36+GF,DF=x+15,即x+15=35+GF,
∴BC=GF=x-21,
在Rt△DBC中,tan∠DBC=$\frac{CD}{BC}$,即$\frac{x}{x-21}$≈2.5,
解得x≈35,
答:坡顶B到地面AE的距离为15米,纪念碑CD的高度约为35米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡度和仰角构造直角三角形,利用三角函数的知识解直角三角形.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
17.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.已知1微米=10-7米,则25微米用科学记数法表示为( )
| A. | 0.25×10-5米 | B. | 25×10-7米 | C. | 2.5×10-6米 | D. | 2.5×10-8米 |
 如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
如图,在Rt△ABC中,∠BCA=90°,CD是AB边上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.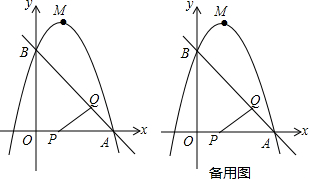
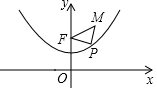 已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )
已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )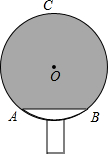 如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.
如图,小明自制一块乒乓球拍,正面是半径为8cm的⊙O,$\widehat{AB}$=90°,弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为(32+48π)cm2.