题目内容
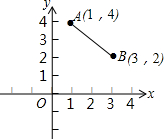 “西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?
“西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:写出点B关于x轴的对称点B′的坐标,用待定系数法求得直线B′A的解析式,再求得B′A与x的交点的坐标,即题意要求的点.然后根据勾股定理即可求得AB′的长,即到两村所铺设的管道最短距离.
解答:
 解:点B关于x轴的对称点B′的坐标为(3,-2),
解:点B关于x轴的对称点B′的坐标为(3,-2),
设直线B′A的解析式为y=kx+b,
得到
,
解得k=-3,b=7,
∴y=-3x+7,
当y=0时,x=
,即点P的坐标为(
,0).
因为PB=PB′,所以PA+PB=PA+PB′=AB′,
根据两点之间线段最短,AB′就是PA+PB的最小值,
AB′=
=2
(千米)
故该供气站应建在(
,0)这个位置,到两村所铺设的管道最少需要2
千米.
 解:点B关于x轴的对称点B′的坐标为(3,-2),
解:点B关于x轴的对称点B′的坐标为(3,-2),设直线B′A的解析式为y=kx+b,
得到
|
解得k=-3,b=7,
∴y=-3x+7,
当y=0时,x=
| 7 |
| 3 |
| 7 |
| 3 |
因为PB=PB′,所以PA+PB=PA+PB′=AB′,
根据两点之间线段最短,AB′就是PA+PB的最小值,
AB′=
| (1-3)2+(4+2)2 |
| 10 |
故该供气站应建在(
| 7 |
| 3 |
| 10 |
点评:本题利用了轴对称图形的性质和用待定系数法确定函数的解析式的方法求解.两点之间线段最短是解题的关键.

练习册系列答案
相关题目
 在三角形ABC中,AB=8,AC=9,BC=10.P0为BC边上的一点,在边AC上取点P1,使得CP1=CP0,在边AB上取点P2,使得AP2=AP1,在边BC上取点P3,使得BP3=BP2,若P0P3=1,则CP0的长度为( )
在三角形ABC中,AB=8,AC=9,BC=10.P0为BC边上的一点,在边AC上取点P1,使得CP1=CP0,在边AB上取点P2,使得AP2=AP1,在边BC上取点P3,使得BP3=BP2,若P0P3=1,则CP0的长度为( )| A、4 | B、6 | C、4或5 | D、5或6 |
已知|a|=5,|b|=8,且满足a+b<0,则a-b的值为( )
| A、-13 | B、13 |
| C、3或13 | D、13或-13 |
下面用数学语言叙述代数式
-b,其中表达不正确的是( )
| 1 |
| a |
| A、比a的倒数小b的数 |
| B、1除以a的商与b的相反数的差 |
| C、1除以a的商与b的相反数的和 |
| D、b与a的倒数的差的相反数 |
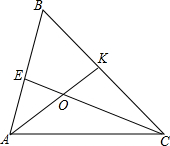 如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.
如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.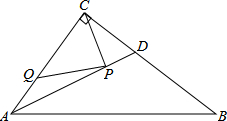 Rt△ABC中,∠ACB=90°,AB=10.BC=8,AD平分∠BAC,P、Q在AD,AC上运动,求PC+PQ的最小值.
Rt△ABC中,∠ACB=90°,AB=10.BC=8,AD平分∠BAC,P、Q在AD,AC上运动,求PC+PQ的最小值. AB=AC,∠1=∠2,∠3=∠4,求证:BE=CF.
AB=AC,∠1=∠2,∠3=∠4,求证:BE=CF.