题目内容
已知a、b、c为三角形ABC的三边长,求证:关于x的方程cx2-(a+b)x+
=0有两个不相等的实数根.
| c |
| 4 |
考点:根的判别式,三角形三边关系
专题:证明题
分析:先根据三角形三边关系得出a+b>c,再计算判别式的值得到△=(a+b)2-c2>0,然后根据判别式的意义即可证明.
解答:
证明:∵a、b、c为△ABC的三条边,
∴a+b>c>0,
∴(a+b)2>c2.
对方程cx2-(a+b)x+
=0来说,
∵△=(a+b)2-c2>0,
∴关于x的方程cx2-(a+b)x+
=0有两个不相等的实数根.
∴a+b>c>0,
∴(a+b)2>c2.
对方程cx2-(a+b)x+
| c |
| 4 |
∵△=(a+b)2-c2>0,
∴关于x的方程cx2-(a+b)x+
| c |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了三角形的三边关系定理.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
某住宅小区6月份随机抽查了该小区6天的用水量(单位:吨),结果分别是30、34、32、37、28、31.那么,请你估计该小区6月份(30天)的总用水量的吨数约是( )
| A、960 | B、192 |
| C、5760 | D、32 |
下列说法错误的是( )
| A、若a=b,则a+1=b+1 | ||||
| B、若a=b,则a(x2+1)=b(x2+1) | ||||
C、若a=b,则
| ||||
| D、若a(x-1)=b(x-1),则a=b |
若a>b,且c为实数,则( )
| A、ac>bc |
| B、ac<bc |
| C、ac2>bc2 |
| D、ac2≥bc2 |
温州某服装店一月份的营业额为8万元,三月份的营业额为10万元.如果平均每月的增长率为x,则由题意可列出方程为( )
| A、8(1+x)2=10 |
| B、8(1-x)2=10 |
| C、8+8×2x=10 |
| D、8+8x2=10 |
已知样本数据1,4,2,3,4,5,这组数据的中位数是( )
| A、3 | B、4 | C、3.5 | D、2.5 |
 如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.
如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.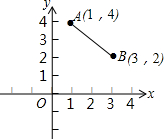 “西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?
“西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?