题目内容
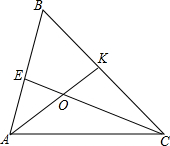 如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.
如图,在△ABC中,∠B=60°,角平分线AK,CE的交点为O.求证:OK=OE.考点:全等三角形的判定与性质
专题:
分析:过O作OM⊥AB,ON⊥BC,垂足分别为M、N,由条件可知O在∠B的平分线上,结合条件可求得∠EOK=∠MON=120°,可得到∠EOM=∠NOK,可证明△EOM≌△KON,可证明OK=OE.
解答:
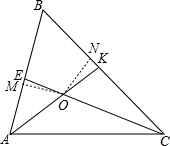 证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
∵AK、CE为角平分线,
∴点O在∠B的平分线上,
∴OM=ON,
∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°,
∵AK平分∠BAC,CE平分∠BCA,
∴∠BAC=2∠OAC,∠BCA=2∠OCA,
∴∠OAC+∠OCA=60°,
∴∠AOC=120°,
∴∠EOK=120°,
在四边形BMON中,∠B=60°,∠BMO=∠BNO=90°,
∴∠MON=120°,
∴∠EOM=∠NOK
在△EOM和△KON中,
,
∴△EOM≌△KON(ASA),
∴OK=OE.
 证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,
证明:如图,过O作OM⊥AB,ON⊥BC,垂足分别为M、N,∵AK、CE为角平分线,
∴点O在∠B的平分线上,
∴OM=ON,
∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°,
∵AK平分∠BAC,CE平分∠BCA,
∴∠BAC=2∠OAC,∠BCA=2∠OCA,
∴∠OAC+∠OCA=60°,
∴∠AOC=120°,
∴∠EOK=120°,
在四边形BMON中,∠B=60°,∠BMO=∠BNO=90°,
∴∠MON=120°,
∴∠EOM=∠NOK
在△EOM和△KON中,
|
∴△EOM≌△KON(ASA),
∴OK=OE.
点评:本题主要考查全等三角形的判定和性质及角平分线的性质,作两边的垂线构造条件证明三角形全等是解题的关键,注意角平分线性质、三角形四边形内角和定理的应用.

练习册系列答案
相关题目
温州某服装店一月份的营业额为8万元,三月份的营业额为10万元.如果平均每月的增长率为x,则由题意可列出方程为( )
| A、8(1+x)2=10 |
| B、8(1-x)2=10 |
| C、8+8×2x=10 |
| D、8+8x2=10 |
已知样本数据1,4,2,3,4,5,这组数据的中位数是( )
| A、3 | B、4 | C、3.5 | D、2.5 |
有一个数值转换器,原理如下:当输入的x为64时,输出的y是( )


| A、8 | ||
B、
| ||
C、
| ||
D、
|
 实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )
实数a、b在数轴上的位置如图所示,则化简|a+b|-a的结果为( )| A、2a+b | B、-b |
| C、-2a-b | D、b |
 如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.
如图所示,在△ABC中,AB=AC,M为BC的中点,MD⊥AB于点D,MD⊥AC于点E.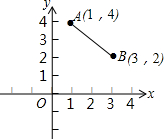 “西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?
“西气东输”惠及千家万户,使许多的农村家庭也告别了以植物秸秆为主要原料的时代,使用上了天然气,如图所示,天然气的主要管道在x轴所在的位置,现拟在该主要管道上新建一气站为图中的A,B两村庄的农户供气,请你帮助确定该供气站建在何处时,到两村所铺设的管道最短,最少需要管道多少千米?