题目内容
17.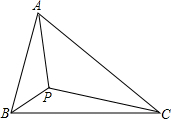 已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP.
已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP.
分析 根据三角形的内角和得到∠CAP+∠ACP=60°,求得∠ACP=60°-∠CAP,由∠BAP=60°-∠CAP,得到∠BAP=∠ACP,证得△ABP∽△ACP,根据相似三角形的性质即可得到结论.
解答 证明:∵∠APB=∠APC=120°,
∴∠CAP+∠ACP=60°,
∴∠ACP=60°-∠CAP,
∵∠BAC=60°,
∴∠BAP=60°-∠CAP,
∴∠BAP=∠ACP,
∴△ABP∽△ACP,
∴$\frac{AP}{PB}=\frac{PC}{AP}$,
∴AP2=BP•CP.
点评 本题考查了相似三角形的判定和性质,三角形的内角和,熟练正确相似三角形的判定定理是解题的关键.

练习册系列答案
相关题目
3.一元二次方程x(x-1)=0的根是( )
| A. | 1 | B. | 0 | C. | 0或1 | D. | 0或-1 |
12.已知实数a,b,c均不为零,且满足a+b+c=0,则$\frac{1}{{b}^{2}+{c}^{2}-{a}^{2}}$+$\frac{1}{{c}^{2}+{a}^{2}-{b}^{2}}$+$\frac{1}{{a}^{2}+{b}^{2}-{c}^{2}}$的值是( )
| A. | 为正 | B. | 为负 | ||
| C. | 为0 | D. | 与a,b,c的取值有关 |
2.某商家试销一种成本为50元/件的T恤,经试销发现:每周销售量y(件)与销售单价x(元/件)符合一次函数关系,试销数据如下表:
(1)求y与x的函数关系式;
(2)若该商场前期投资2000元装修门面,则第一周扣除投资和成本后是盈利还是亏损,并求出最多盈利(或最少亏损)多少元?
(3)若在第一周里,按盈利最大(或最少亏损)的销售单价进行销售后,在第二周物价部门进行了干预,规定试销期间单价不低于成本单价,获利又不得高于60%.则该商家经过这两周的营销,要在全部收回投资的基础上使利润达到975元,那么第二周应该确定销售单价为多少元?
| 售价(元/件) | … | 55 | 60 | 70 | … |
| 销量(件) | … | 75 | 70 | 60 | … |
(2)若该商场前期投资2000元装修门面,则第一周扣除投资和成本后是盈利还是亏损,并求出最多盈利(或最少亏损)多少元?
(3)若在第一周里,按盈利最大(或最少亏损)的销售单价进行销售后,在第二周物价部门进行了干预,规定试销期间单价不低于成本单价,获利又不得高于60%.则该商家经过这两周的营销,要在全部收回投资的基础上使利润达到975元,那么第二周应该确定销售单价为多少元?
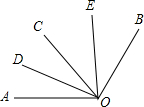 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.