题目内容
5.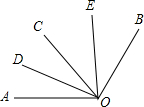 如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.
如图,已知∠AOC=60°,∠BOC=70°,且OD平分∠AOC,OE平分∠BOC.(1)求出∠AOB及其补角的度数;
(2)求出∠COD和∠AOE的度数,判断∠DOE与∠AOB是否互补,并说明理由.
分析 (1)∠AOB的度数等于已知两角的和,再根据补角的定义求解;
(2)根据角平分线把角分成两个相等的角,求出度数后即可判断.
解答 解:(1)∠AOB=∠BOC+∠AOC=70°+60°=130°,
其补角为180°-∠AOB=180°-130°=50°;
(2)∠DOC=$\frac{1}{2}$×∠BOC=$\frac{1}{2}$×70°=35°
∠AOE=$\frac{1}{2}$×∠AOC=$\frac{1}{2}$×60°=30°.
∠DOE与∠AOB不互补,
理由:∵∠DOE=∠DOC+∠COE=35°+30°=65°,
∴∠DOE+∠AOB=65°+130°=195°,
故∠DOE与∠AOB不互补.
点评 本题主要考查角平分线的定义和补角的定义,关键是根据根据补角的定义解答.

练习册系列答案
相关题目
11.以下各正方形的边长是无理数的是( )
| A. | 面积为3的正方形 | B. | 面积为1.44的正方形 | ||
| C. | 面积为25的正方形 | D. | 面积为16的正方形 |

 如图,AB与CD相交于点E,EF⊥AB,∠1=30°,则∠2=60°.
如图,AB与CD相交于点E,EF⊥AB,∠1=30°,则∠2=60°. 如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.
如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.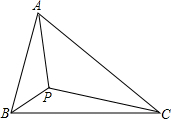 已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP.
已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP. 如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE=3.
如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=11,AC=5,则BE=3.