题目内容
12.已知实数a,b,c均不为零,且满足a+b+c=0,则$\frac{1}{{b}^{2}+{c}^{2}-{a}^{2}}$+$\frac{1}{{c}^{2}+{a}^{2}-{b}^{2}}$+$\frac{1}{{a}^{2}+{b}^{2}-{c}^{2}}$的值是( )| A. | 为正 | B. | 为负 | ||
| C. | 为0 | D. | 与a,b,c的取值有关 |
分析 根据a+b+c=0,可得b+c=-a,c+a=-b,a+b=-c,从而可以将$\frac{1}{{b}^{2}+{c}^{2}-{a}^{2}}$+$\frac{1}{{c}^{2}+{a}^{2}-{b}^{2}}$+$\frac{1}{{a}^{2}+{b}^{2}-{c}^{2}}$化简求值,从而解答本题.
解答 解:∵a+b+c=0,
∴b+c=-a,c+a=-b,a+b=-c,
∴$\frac{1}{{b}^{2}+{c}^{2}-{a}^{2}}$+$\frac{1}{{c}^{2}+{a}^{2}-{b}^{2}}$+$\frac{1}{{a}^{2}+{b}^{2}-{c}^{2}}$
=$\frac{1}{(b+c)^{2}-2bc-{a}^{2}}+\frac{1}{(c+a)^{2}-2ac-{b}^{2}}$+$\frac{1}{(a+b)^{2}-2ab-{c}^{2}}$
=$\frac{1}{{a}^{2}-2bc-{a}^{2}}+\frac{1}{{b}^{2}-2ac-{b}^{2}}$+$\frac{1}{{c}^{2}-2ab-{c}^{2}}$
=$\frac{1}{-2bc}+\frac{1}{-2ac}+\frac{1}{-2ab}$
=$-\frac{1}{2}×(\frac{1}{bc}+\frac{1}{ac}+\frac{1}{ab})$
=$-\frac{1}{2}×\frac{a+b+c}{abc}$
=0.
故选C.
点评 本题考查分式的化简求值,解题的关键是可以运用题目中的式子灵活变化求出所求式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.点P为直线MN外一点,点A、B、C为直线MN上三点,PA=4厘米,PB=5厘米,PC=2厘米,则P到直线MN的距离为( )
| A. | 4厘米 | B. | 2厘米 | C. | 小于2厘米 | D. | 不大于2厘米 |
7.-5的绝对值的相反数的倒数是( )
| A. | -$\frac{1}{5}$ | B. | -5 | C. | 5 | D. | $\frac{1}{5}$ |
1.无论x、y取任何值,多边形x2+y2-2x-4y+6的值总是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
 如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.
如图,正方形ABCD的面积为10,点E为边BC上一动点(点E不与B、C重合),联结AE,以CE为边长作小正方形CEFG,点G在边CD上.设BE=x.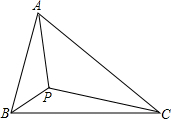 已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP.
已知△ABC中,∠CAB=60°,P为△ABC内一点且∠APB=∠APC=120°,求证:AP2=BP•CP.