题目内容
3．一元二次方程x（x-1）=0的根是（ ）| A． | 1 | B． | 0 | C． | 0或1 | D． | 0或-1 |
分析 利用因式分解法把原方程转化为x=0或x-1=0，然后解两个一次方程即可．
解答 解：x=0或x-1=0，
所以x1=0，x2=1．
故选C．
点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
练习册系列答案
相关题目
14．计算（-$\frac{1}{3}$）×3的结果是（ ）
| A． | -1 | B． | -2 | C． | 2 | D． | -$\frac{2}{3}$ |
11．以下各正方形的边长是无理数的是（ ）
| A． | 面积为3的正方形 | B． | 面积为1.44的正方形 | ||
| C． | 面积为25的正方形 | D． | 面积为16的正方形 |
15．党的十八届三中全会决定提出研究制定渐进式延迟退休年龄的政策，最近人社部新闻发言中心对延迟退休年龄进行了回应称：每年只会延长几个月．
渐进式退休年龄应该怎么算？《假定从2022年起实施延迟退休》
以55岁退休为标准，假定每年延长退休时间为6个月，自方案实施起，逐渐累计递增，直到达到新拟定的退休年龄，网友据此只做了一张“延迟退休对照表”．
（1）根据上表，1974年出生的人实际退休年龄将会是59岁；
（2）若每年延迟退休3个月，则2006年出生的人恰好是65岁退休．
渐进式退休年龄应该怎么算？《假定从2022年起实施延迟退休》
以55岁退休为标准，假定每年延长退休时间为6个月，自方案实施起，逐渐累计递增，直到达到新拟定的退休年龄，网友据此只做了一张“延迟退休对照表”．
| 出生年份 | 2022年年龄（岁） | 延迟退休时间（年） | 实际退休年龄（岁） |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
（2）若每年延迟退休3个月，则2006年出生的人恰好是65岁退休．
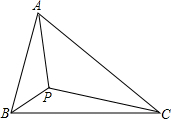已知△ABC中，∠CAB=60°，P为△ABC内一点且∠APB=∠APC=120°，求证：AP2=BP•CP．