题目内容
2.操作:折叠纸片,并将折叠后的部分压平在纸片原来所在平面内.研究一:
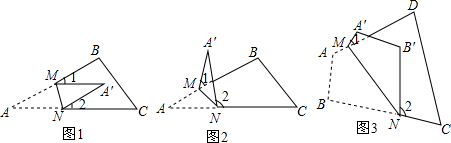
(1)将△ABC纸片沿直线MN折叠成图1的形状,则∠1、∠2与∠A之间的数量关系为∠1+∠2=2∠A(不需要说明理由).
(2)将△ABC纸片沿直线MN折成图2的形状,则∠1、∠2和∠A之间存在怎样的数量关系?请试着找出来,并说明理由.
研究二:将四边形ABCD(AD与BC不平行)沿直线MN折叠成图3的形状,则∠1、∠2与∠A、∠B之间的数量关系是∠1+∠2=2(∠A+∠B)-360°(请将含∠1、∠2的项放在等式的左边,其余各项放在等式的右边),并说明理由.
分析 (1)根据三角形的外角的性质即可得到结论;
(2)连接AA′构造等腰三角形,然后结合三角形的外角性质进行探讨证明;
(3)根据平角的定义以及四边形的内角和定理进行探讨.
解答 解:(1)如图1,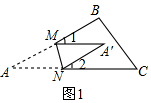
由图形折叠的性质可知,∠CNA′=180°-2∠DNA′…①,∠BMA′=180°-2∠A′MN…②,
①+②得,∠BMA′+∠CNA′=360°-2(∠DNA′+∠A′MN)
即∠BMA′+∠CNA′=360°-2(180°-∠A),
故∠1+∠2=2∠A;
(2)∠2-∠1=2∠A.
证明如下:
如图2,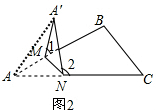
连接AA′构造等腰三角形,
∠BMA′=2∠MA'A,∠CNA'=2∠NA'A,
得∠2-∠1=2∠A,
(3)如图③,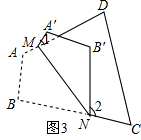
由图形折叠的性质可知∠1=180°-2∠AMN,∠2=180°-2∠BNM,
两式相加得,∠1+∠2=360°-2(∠AMN+∠BNM)
即∠1+∠2=360°-2(360°-∠A-∠B),
所以,∠1+∠2=2(∠A+∠B)-360°.
点评 此题考查三角形的内角和定理,注意此类一题多变的题型,基本思路是相同的,主要运用三角形的内角和定理及其推论进行证明.

练习册系列答案
相关题目
12.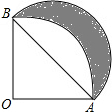 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
10.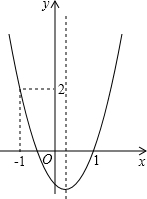 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+bm<m(am+b);④(a+c)2<b2;⑤a>1.其中正确的是( )| A. | ①⑤ | B. | ①②⑤ | C. | ②⑤ | D. | ①③④ |
7.暑假快到了,父母找算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一款游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
| A. | 掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢 | |
| B. | 同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢 | |
| C. | 掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢 | |
| D. | 在不透明的袋子中装有两黑两红四个球,除颜色外,其余均相同,随机摸出一个是黑球则哥哥赢,是红球则妹妹赢 |
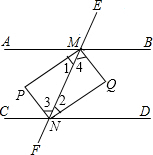 已知:如图,直线AB∥CD,EF和AB、CD分别相交于M、N两点,射线MP、MQ、NP、NQ分别是∠AMN、∠BMN、∠MNC、∠MND的平分线,MP、NP相交于点P,MQ和NQ相交于点Q,求证:四边形MPNQ是矩形.
已知:如图,直线AB∥CD,EF和AB、CD分别相交于M、N两点,射线MP、MQ、NP、NQ分别是∠AMN、∠BMN、∠MNC、∠MND的平分线,MP、NP相交于点P,MQ和NQ相交于点Q,求证:四边形MPNQ是矩形.