题目内容
12.化简:$\frac{1-\sqrt{2}+\sqrt{3}}{1+\sqrt{2}-\sqrt{3}}$.分析 首先将原式分子分母同乘以1$+\sqrt{2}+\sqrt{3}$,利用平方差公式计算,再分母有理化.
解答 解:原式=$\frac{(1-\sqrt{2}+\sqrt{3})(1+\sqrt{2}+\sqrt{3})}{(1+\sqrt{2}-\sqrt{3})(1+\sqrt{2}+\sqrt{3})}$
=$\frac{{(1+\sqrt{3})}^{2}{-(\sqrt{2})}^{2}}{{(1+\sqrt{2})}^{2}{-(\sqrt{3})}^{2}}$
=$\frac{4+2\sqrt{3}-2}{3+2\sqrt{2}-3}$
=$\frac{2+2\sqrt{3}}{2\sqrt{2}}$
=$\frac{1+\sqrt{3}}{\sqrt{2}}$
=$\frac{\sqrt{2}+\sqrt{6}}{2}$.
点评 本题主要考查了二次根式的化简求值,分子分母同乘以有理化因式(1$+\sqrt{2}+\sqrt{3}$)是解答此题的关键.

练习册系列答案
相关题目
4.设一元二次方程x2-2x-4=0的两个实根为x1和x2,则下列结论正确的是( )
| A. | x1+x2=-4 | B. | x1+2=4 | C. | x1+x2=2 | D. | x1+2=-2 |
1.为筹备班级的庆祝国庆60周年联欢会,班长对全班学生爱吃哪几种水果进行民意调查那么最终买什么水果,下面的调查数据中最值得关心的是( )
| A. | 中位数 | B. | 平均数 | C. | 众数 | D. | 加权平均数 |
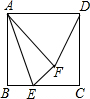 如图,在正方形ABCD中的边长为6,E为BC上一点,CE=2BE,将△ABE沿AE折叠的△AFE,连接DF,则线段DF的长度为$\frac{12\sqrt{5}}{5}$.
如图,在正方形ABCD中的边长为6,E为BC上一点,CE=2BE,将△ABE沿AE折叠的△AFE,连接DF,则线段DF的长度为$\frac{12\sqrt{5}}{5}$.