题目内容
12．
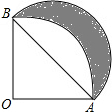如图，扇形AOB的半径为1，∠AOB=90°，以AB为直径画半圆，则图中的阴影部分的面积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$π | C． | $\frac{1}{8}$π | D． | π |
分析 根据阴影部分的面积=△AOB的面积+半圆的面积-扇形AOB的面积和扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$计算即可．
解答 解：扇形AOB的半径为1，∠AOB=90°，
∴AB=$\sqrt{2}$，
阴影部分的面积=$\frac{1}{2}$×1×1+$\frac{1}{2}$π×（$\frac{\sqrt{2}}{2}$）2-$\frac{90π×{1}^{2}}{360}$
=$\frac{1}{2}$+$\frac{1}{4}$π-$\frac{1}{4}$π
=$\frac{1}{2}$
故选：A．
点评 本题考查的是阴影面积的计算，掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键．
练习册系列答案
相关题目
2．把抛物线y=$\frac{1}{2}$（x-4）2先向左平移3个单位，再向下平移4个单位，所得到的抛物线是（ ）
| A． | y=$\frac{1}{2}$（x-4）2-4 | B． | y=$\frac{1}{2}$x2 | C． | y=$\frac{1}{2}$（x-7）2-4 | D． | y=$\frac{1}{2}$（x-1）2-4 |
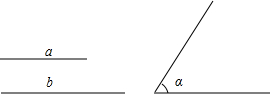如图，已知：线段a，b和∠α．求作：△ABC，使∠BAC=∠α，高线AD=a，角平分线AE=b．
已知：在锐角三角形ABC中，O是外心，H是垂心，O′，O″是O关于AB，AC的对称点，求证：四边形AO′HO″是菱形．
如图，△ABC中，D、E、F为BC、AD、BE的中点，若△CEF的面积是3，则△ABC的面积是12．