题目内容
10.直角三角形的两条直角边分别为a,b,斜边为c,一个圆与这个直角三角形的斜边相切,与两条直角边所在的直线相切,则这个圆的半径为$\frac{a+b-c}{2}$或$\frac{a+b+c}{2}$.分析 分两种情形分别求解即可.当⊙O在△ABC内部时,设切点分别为E、F、D.由切线长定理可知,AE=AD,CF=CD,BE=BF,易知四边形BFOE是正方形,可得OE=BE=$\frac{AB+BC-AC}{2}$=$\frac{a+b-c}{2}$.当⊙O在△ABC外部时,同法可求.
解答 解:当⊙O在△ABC内部时,设切点分别为E、F、D.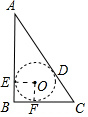
由切线长定理可知,AE=AD,CF=CD,BE=BF,
易知四边形BFOE是正方形,
∴OE=BE=$\frac{AB+BC-AC}{2}$=$\frac{a+b-c}{2}$.
当⊙O在△ABC外部时,设切点为E、D、F.则四边形OEBF是正方形.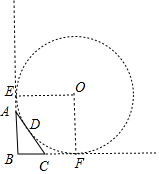
由切线长定理可知OE=BE=$\frac{AB+BC+AC}{2}$=$\frac{a+b+c}{2}$,
故答案为$\frac{a+b-c}{2}$或$\frac{a+b+c}{2}$.
点评 本题考查切线的性质、切线长定理.正方形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
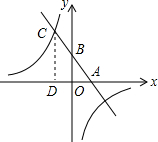 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.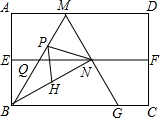 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展开后再过点B折叠矩形纸片,使按A落在EF上的点N,折痕BM与EF相交于点Q,再次展平,连接BN,MN,延长MN交BC于点G.