题目内容
4．计算（-xy3）2•（-$\frac{1}{2}$xy2）的结果是-$\frac{1}{2}$x3y8．分析 首先利用积的乘方运算法则将原式变形，进而结合单项式乘以单项式计算得出答案．
解答 解：（-xy3）2•（-$\frac{1}{2}$xy2）
=x2y6×（-$\frac{1}{2}$xy2）
=-$\frac{1}{2}$x3y8．
点评 此题主要考查了单项式乘以单项式以及积的乘方运算，正确掌握相关运算法则是解题关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
14．已知下列命题：
①若m＞n，则m2＞n2
②垂直于弦的直径平分弦
③对角线互相平分且相等的四边形是菱形
④如果两条弧相等，那么它们所对的圆心角相等
⑤若a≤0，则|a|=-a
⑥若a＞0，则$\sqrt{{a}^{2}}$=a
其中，原命题与逆命题全为真命题的个数是（ ）
①若m＞n，则m2＞n2
②垂直于弦的直径平分弦
③对角线互相平分且相等的四边形是菱形
④如果两条弧相等，那么它们所对的圆心角相等
⑤若a≤0，则|a|=-a
⑥若a＞0，则$\sqrt{{a}^{2}}$=a
其中，原命题与逆命题全为真命题的个数是（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
12．
在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2017OB2017．则点B2017的坐标（ ）
在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2017OB2017．则点B2017的坐标（ ）| A． | （22017，-22017） | B． | （22016，-22016） | C． | （22017，22017） | D． | （22016，22016） |
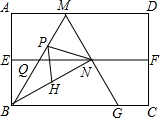如图，四边形ABCD是矩形纸片，AB=2，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，展开后再过点B折叠矩形纸片，使按A落在EF上的点N，折痕BM与EF相交于点Q，再次展平，连接BN，MN，延长MN交BC于点G．
9．已知n个数据的和为108，平均数为12，则n为（ ）
| A． | 7 | B． | 8 | C． | 9 | D． | 10 |
16．下列二次根式，不能与$\sqrt{2}$合并的是（ ）
| A． | $\sqrt{\frac{1}{2}}$ | B． | $\sqrt{8}$ | C． | $\sqrt{12}$ | D． | -$\sqrt{18}$ |
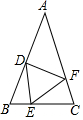如图，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，且BE=CF，AD+EC=AB．
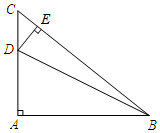如图，在等腰Rt△ABC中，∠A=90°，AC=6，D是AC上一点，过D作DE⊥BC于点E，若$tan∠DBA=\frac{1}{5}$，则CE的长为$\frac{12\sqrt{2}}{5}$．