题目内容
11．甲、乙两名运动员在某项射击比赛中10次射击的平均成绩都是7环，而甲、乙的成绩的方差分别为1.21和3.12，由此可知（ ）| A． | 甲比乙的成绩稳定 | B． | 乙比甲的成绩稳定 | ||
| C． | 甲、乙的成绩一样稳定 | D． | 无法确定谁的成绩更稳定 |
分析 根据方差的定义，方差越小数据越稳定．
解答 解：因为S甲2=1.21＜S乙2=3.12，方差小的为甲，
所以本题中成绩比较稳定的是甲．
故选A．
点评 本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
练习册系列答案
阅读快车系列答案
相关题目
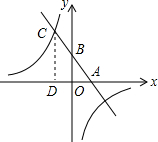已知，如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数xy=n（n为常数且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂直为D．若OB=2OA=3OD=6．则反比例函数的解析式为y=-$\frac{20}{x}$．
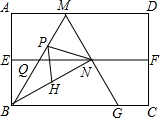如图，四边形ABCD是矩形纸片，AB=2，对折矩形纸片ABCD，使AD与BC重合，折痕为EF，展开后再过点B折叠矩形纸片，使按A落在EF上的点N，折痕BM与EF相交于点Q，再次展平，连接BN，MN，延长MN交BC于点G．
6．平行四边形的一个角比它的邻角的2倍还大15°，则相邻两个角为（ ）
| A． | 30°，75° | B． | 40°，95° | C． | 50°，115° | D． | 55°，125° |
16．下列二次根式，不能与$\sqrt{2}$合并的是（ ）
| A． | $\sqrt{\frac{1}{2}}$ | B． | $\sqrt{8}$ | C． | $\sqrt{12}$ | D． | -$\sqrt{18}$ |
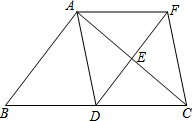如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接AD、CF．
19．下列各式中正确的是（ ）
| A． | $\sqrt{\frac{a}{2{b}^{2}}}$=$\frac{1}{2b}$$\sqrt{a}$（b＞0） | B． | $\sqrt{\frac{7x}{12{y}^{3}}}$=$\frac{1}{6{y}^{2}}$$\sqrt{21xy}$ | ||
| C． | $\sqrt{{a}^{2}+{b}^{2}}$=a+b（a≥0，b≥0） | D． | 5$\sqrt{\frac{2a}{5}}$=$\sqrt{2a}$ |