题目内容
13.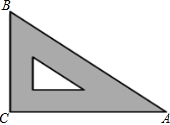 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )| A. | 30$\sqrt{3}$cm | B. | 20$\sqrt{3}$cm | C. | 10$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
分析 因为教学用的直角三角板为直角三角形,所以利用三角函数定义,一个角的正切值等于这个角的对边比邻边可知角BAC的对边为BC,邻边为AC,根据角BAC的正切值,即可求出BC的长度.
解答 解:∵直角△ABC中,∠C=90°,
∴tan∠BAC=$\frac{BC}{AC}$,
又∵AC=30cm,tan∠BAC=$\frac{\sqrt{3}}{3}$,
∴BC=AC•tan∠BAC=30×$\frac{\sqrt{3}}{3}$=10$\sqrt{3}$(cm).
故选C.
点评 此题考查解直角三角形,锐角三角函数的定义,熟知tan∠BAC=$\frac{BC}{AC}$是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.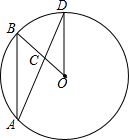 如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
 如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
18.位似图形的位似中心可以在( )
| A. | 原图形外 | B. | 原图形内 | C. | 原图形的边上 | D. | 以上三种都可以 |
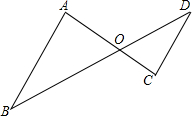 如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么?
如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么? 有一个长、宽、高分别为12cm,4cm,3cm的长方体铁盒,铁盒内能放入的最长的木棒长为多少?
有一个长、宽、高分别为12cm,4cm,3cm的长方体铁盒,铁盒内能放入的最长的木棒长为多少?
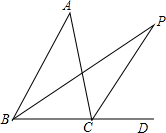 如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.