题目内容
1．
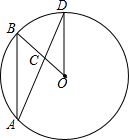如图所示，在⊙O中，∠BOD=30°，OD∥AB，AD，OB相交于点C，那么∠BCD的度数是（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
分析 根据圆周角定理求出∠A的度数，根据平行线的性质求出∠D的度数，根据三角形的外角的性质计算得到答案．
解答 解：∠A=$\frac{1}{2}$∠BOD=15°，
∵OD∥AB，
∴∠D=∠A=15°，
∴∠BCD=∠BOD+∠D=45°，
故选：C．
点评 本题考查的是圆周角定理和三角形的外角的性质，掌握同弧所对的圆周角是圆心角的一半是解题的关键．
练习册系列答案
相关题目
12．李明的家在汽车站（O）的东偏北18°方向500米的A处，学校B在汽车站（O）的南偏西10°方向600米处，李明上学经汽车站所走的角∠AOB=（ ）
| A． | 28° | B． | 108° | C． | 118° | D． | 98° |
16．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，则它的外接圆的半径为（ ）
| A． | 1.5cm | B． | 2cm | C． | 2.5cm | D． | 3cm |
6．判断下列四组数据，不可以作为直角三角形三条边的是（ ）
| A． | 4，3，5 | B． | 0.3，0.4，0.5 | C． | 1，2，3 | D． | 8，15，17 |
13．
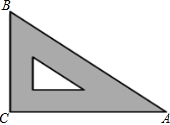如图是教学用直角三角板，边AC=30cm，∠C=90°，tan∠BAC=$\frac{\sqrt{3}}{3}$，则边BC的长为（ ）
如图是教学用直角三角板，边AC=30cm，∠C=90°，tan∠BAC=$\frac{\sqrt{3}}{3}$，则边BC的长为（ ）| A． | 30$\sqrt{3}$cm | B． | 20$\sqrt{3}$cm | C． | 10$\sqrt{3}$cm | D． | 5$\sqrt{3}$cm |
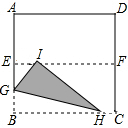如图，将边长为4的正方形ABCD对折后展开，折痕为EF，分别在边AB、BC上取点G、H，沿GH对折，使点B落在折痕EF上，落点记为I，则：