题目内容
4.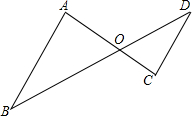 如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么?
如图,若∠A=∠C,那么△OAB与△OCD相似吗?有OA•OD=OB•OC吗?为什么?
分析 运用两个三角形两个角相等,得出△OAD∽△OCB;根据两边对应成比例且夹角相等,得到△OAD∽△OCB.
解答 解:△OAB与△OCD相似,
理由:∵∠A=∠C,∠AOD=∠BOC,
∴△OAD∽△OCB;
△OAB与△OCD相似,
理由:∵OA•OD=OB•OC,
∴$\frac{OA}{OC}=\frac{OB}{OD}$,
∵∠AOB=∠COD,
∴△OAB∽△OCD.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质定理是解题的关键.

练习册系列答案
相关题目
12.李明的家在汽车站(O)的东偏北18°方向500米的A处,学校B在汽车站(O)的南偏西10°方向600米处,李明上学经汽车站所走的角∠AOB=( )
| A. | 28° | B. | 108° | C. | 118° | D. | 98° |
16.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则它的外接圆的半径为( )
| A. | 1.5cm | B. | 2cm | C. | 2.5cm | D. | 3cm |
13.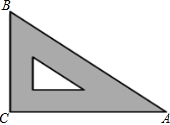 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )| A. | 30$\sqrt{3}$cm | B. | 20$\sqrt{3}$cm | C. | 10$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
 如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.