题目内容
2.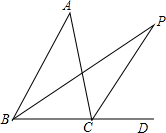 如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
分析 根据∠ACD=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC=$\frac{1}{2}$∠ABC,∠PCA=$\frac{1}{2}$∠ACD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到$\frac{1}{2}$∠A即可.
解答 解:∵CP平分∠ACD,BP平分∠ABC,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCA=$\frac{1}{2}$∠ACD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
∵∠P=180°-(∠PBC+∠PCA+∠ACB)=$\frac{1}{2}$∠A=20°.
点评 本题主要考查对三角形的内角和定理,三角形的外角,角平分线的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
12.李明的家在汽车站(O)的东偏北18°方向500米的A处,学校B在汽车站(O)的南偏西10°方向600米处,李明上学经汽车站所走的角∠AOB=( )
| A. | 28° | B. | 108° | C. | 118° | D. | 98° |
13.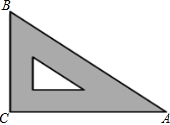 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )| A. | 30$\sqrt{3}$cm | B. | 20$\sqrt{3}$cm | C. | 10$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
12.上午9时,一艘船从A处出发以每小时20海里的速度向正北方向航行,11时到达B处,若在A处测得灯塔C在北偏西34°,且∠ACB=$\frac{3}{2}$∠BAC,则在B处测得灯塔C应为( )
| A. | 北偏西68° | B. | 南偏西85° | C. | 北偏西85° | D. | 南偏西68° |
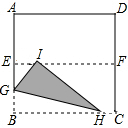 如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
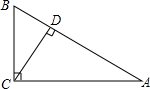 如图,在Rt△ABC中.∠ACB=90°.CD⊥AB于D,若3BC=2AD,求tan∠BCD.
如图,在Rt△ABC中.∠ACB=90°.CD⊥AB于D,若3BC=2AD,求tan∠BCD. 如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.
如图.△ABC中,∠B=∠C,点P、Q、R分别在AB、BC、AC上,且PB=QC,QB=RC.