题目内容
5．如图是面积分别为1，2，3，…，2015的正方形．边长是有理数的正方形有44个．
分析 根据正方形的面积公式先求出边长，然后根据有理数的定义分别进行解答即可．
解答 解：根据S正方形=a2，
可求出边长分别是：1，$\sqrt{2}$，$\sqrt{3}$，2，$\sqrt{5}$，$\sqrt{6}$，$\sqrt{7}$，$\sqrt{8}$，3…，
则边长是有理数的正方形有44个；
故答案为：44．
点评 此题考查了图形的变化类，用到的知识点是正方形的面积公式和有理数的定义，关键是找出2015在哪两个数的平方之间．
练习册系列答案
相关题目
16．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，则它的外接圆的半径为（ ）
| A． | 1.5cm | B． | 2cm | C． | 2.5cm | D． | 3cm |
13．
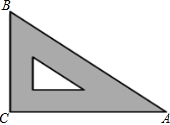如图是教学用直角三角板，边AC=30cm，∠C=90°，tan∠BAC=$\frac{\sqrt{3}}{3}$，则边BC的长为（ ）
如图是教学用直角三角板，边AC=30cm，∠C=90°，tan∠BAC=$\frac{\sqrt{3}}{3}$，则边BC的长为（ ）| A． | 30$\sqrt{3}$cm | B． | 20$\sqrt{3}$cm | C． | 10$\sqrt{3}$cm | D． | 5$\sqrt{3}$cm |
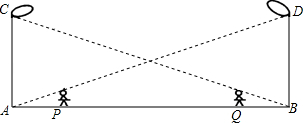如图所示，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶点刚好接触到路灯AC的底部，当他向前再走行20m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学身高是1.5m，两个路灯的高度都是9m，则两路灯之间的距离是多少？
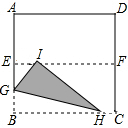如图，将边长为4的正方形ABCD对折后展开，折痕为EF，分别在边AB、BC上取点G、H，沿GH对折，使点B落在折痕EF上，落点记为I，则：
如图．△ABC中，∠B=∠C，点P、Q、R分别在AB、BC、AC上，且PB=QC，QB=RC．