��Ŀ����
19���ⷽ��x2-2x+3-$\frac{6}{{{x^2}-2x+3}}$=1ʱ������x2-2x+3=y����ԭ���̿ɻ�Ϊy-$\frac{6}{y}$=1��ȥ��ĸ����y1=-2��y2=3����y=-2ʱ��x2-2x+3=-2�������0���˷����⣬��y=3ʱ��x2-2x+3=3�����x1=0��x2=2��������x2+3x-$\frac{3}{{{x^2}+3x-7}}$=9�����и��ij˻�Ϊ24������ ��x2+3x-7=y����ԭ���̿ɻ�Ϊy-$\frac{3}{y}$=2�����y1=-1��y2=3����y=-1ʱ��x2+3x-7=-1�����ݸ���ϵ���Ĺ�ϵ���x1•x2=-6����y=3ʱ��x2+3x-7=3�����ݸ���ϵ���Ĺ�ϵ���x3•x4=-4������������и��ij˻�Ϊ24��
��� �⣺x2+3x-$\frac{3}{{{x^2}+3x-7}}$=9��
��x2+3x-7=y����ԭ���̿ɻ�Ϊy-$\frac{3}{y}$=2��
������ʽ����Ϊ��y2-2y-3=0��
���y1=-1��y2=3��
��y=-1ʱ��x2+3x-7=-1����x2+3x-6=0��
�ߡ���0��
��x1•x2=-6��
��y=3ʱ��x2+3x-7=3����x2+3x-4=0��
�ߡ���0��
��x3•x4=-4��
��x1•x2•x3•x4=24��
�ʴ�Ϊ24��
���� ���⿼���˻�Ԫ�����ʽ���̣��û�Ԫ����һЩ���ӵķ�ʽ�����DZȽϼ�һ�ַ��������ݷ����ص������Ӧδ֪�����ⷽ���ܹ�ʹ�������ע��������̽��Ҫ�����

��ϰ��ϵ�д�
�����Ŀ
14������-$\sqrt{5}$��x��$\sqrt{3}$������x�ǣ�������
| A�� | -2��1��0��1��2 | B�� | -1��0��1��2��3 | C�� | -2��-1��0��1 | D�� | -1��0��1��2 |
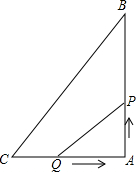 ��ͼ���ڡ�ABC�У���BAC=90�㣬AB=4cm��AC=3cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��2cm/s���ٶ����յ�B�ƶ�����Q��1cm/s���ٶ����յ�A�ƶ�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶���ʱ��Ϊt�룮
��ͼ���ڡ�ABC�У���BAC=90�㣬AB=4cm��AC=3cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��2cm/s���ٶ����յ�B�ƶ�����Q��1cm/s���ٶ����յ�A�ƶ�������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶���ʱ��Ϊt�룮 С�������ij������AB�ĸ߶ȣ���C����ý����ﶥ��A������Ϊ30�㣬Ȼ����CBǰ��100����D������ö���A������Ϊ60�㣬������AB�ĸ߶ȣ�������������ţ�
С�������ij������AB�ĸ߶ȣ���C����ý����ﶥ��A������Ϊ30�㣬Ȼ����CBǰ��100����D������ö���A������Ϊ60�㣬������AB�ĸ߶ȣ�������������ţ�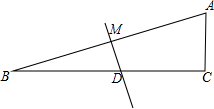 ��ͼ���ڡ�ABC�У���C=90�㣬��B=15�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�M��BD=8cm����AC�ij���
��ͼ���ڡ�ABC�У���C=90�㣬��B=15�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�M��BD=8cm����AC�ij���