题目内容
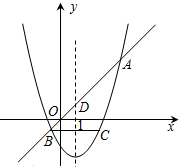 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
| 3 |
| 2 |
(1)求抛物线的解析式;
(2)求A、B两点的坐标及BC的长.
考点:二次函数综合题
专题:
分析:(1)根据抛物线的对称轴方程x=1,可求出m的值,进而可求出抛物线的解析式;
(2)BC平行于x轴,且∠ABC=45°,所以直线y=kx+b与x轴的正半轴或负半轴所成的角为45°,因而,直线y=kx+b与直线y=x或y=-x平行,即k=1或k=-1.
又直线y=kx+b经过点D(1,1),所以可求出直线的解析式,在分两种情况分别讨论不同情况下的直线解析式即可求出A和B的坐标,进而求出BC的长.
(2)BC平行于x轴,且∠ABC=45°,所以直线y=kx+b与x轴的正半轴或负半轴所成的角为45°,因而,直线y=kx+b与直线y=x或y=-x平行,即k=1或k=-1.
又直线y=kx+b经过点D(1,1),所以可求出直线的解析式,在分两种情况分别讨论不同情况下的直线解析式即可求出A和B的坐标,进而求出BC的长.
解答: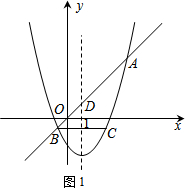 解:(1)据题意有-
解:(1)据题意有-
=1,
∴m=-1.
即抛物线的解析式为y=
x2-x-
.
(2)∵BC平行于x轴,且∠ABC=45°,
∴直线y=kx+b与x轴的正半轴或负半轴所成的角为45°.
因而,直线y=kx+b与直线y=x或y=-x平行.
即k=1或k=-1.
又∵直线y=kx+b经过点D(1,1),
∴1=1+b或1=-1+b,得b=0或b=2,
即直线y=kx+b的解析式为y=x或y=-x+2.
当直线y=kx+b的解析式为y=x时(如图1)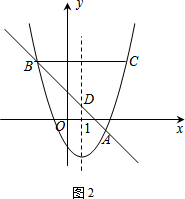
由x═
x2-x-
得x1=2+
,x2=2-
.
∵点B在y轴的左侧,
∴A、B两点的坐标分别为(2+
,2+
),(2-
,2-
).
此时,BC的长为2[1-(2-
)]=2
-2.
当直线y=kx+b的解析式为y=-x+2(如图2)
由-x+2=
x2-x-
,得x1=
,x2=
.
∵点B在y轴的左侧,
∴A、B两点的坐标分别为(
,-
+2)、(-
,
+2).
此时,BC的长为2[1-(-
)]=2
+2.
 解:(1)据题意有-
解:(1)据题意有-| m | ||
2×
|
∴m=-1.
即抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)∵BC平行于x轴,且∠ABC=45°,
∴直线y=kx+b与x轴的正半轴或负半轴所成的角为45°.
因而,直线y=kx+b与直线y=x或y=-x平行.
即k=1或k=-1.
又∵直线y=kx+b经过点D(1,1),
∴1=1+b或1=-1+b,得b=0或b=2,
即直线y=kx+b的解析式为y=x或y=-x+2.
当直线y=kx+b的解析式为y=x时(如图1)

由x═
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 7 |
∵点B在y轴的左侧,
∴A、B两点的坐标分别为(2+
| 7 |
| 7 |
| 7 |
| 7 |
此时,BC的长为2[1-(2-
| 7 |
| 7 |
当直线y=kx+b的解析式为y=-x+2(如图2)
由-x+2=
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 7 |
∵点B在y轴的左侧,
∴A、B两点的坐标分别为(
| 7 |
| 7 |
| 7 |
| 7 |
此时,BC的长为2[1-(-
| 7 |
| 7 |
点评:此题主要考查了二次函数解析式的确定、一次函数的解析式确定、函数图象交点坐标的求法,同时考虑了分类讨论的数学思想,难度较大.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下面各组数是三角形的三边的长,则能构成直角三角形的是( )
| A、2,2,3 |
| B、60,80,100 |
| C、4,5,6 |
| D、5,6,7 |
 在Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于点E,EF⊥AC于点F,求证:AC2=2EF2.
在Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于点E,EF⊥AC于点F,求证:AC2=2EF2. 在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD.
在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD. 如图,直线AB∥CD,P是CD上一点,PG交AB于E,PH交AB于F,且∠EPF=90°,如果∠FPD=50°,则∠PEF的度数为
如图,直线AB∥CD,P是CD上一点,PG交AB于E,PH交AB于F,且∠EPF=90°,如果∠FPD=50°,则∠PEF的度数为