题目内容
设n为自然数,方程x2+(n+1)x+n2=0的两根为αn、βn,求:
+
+…+
.
| 1 |
| (α2+1)(β2+1) |
| 1 |
| (α3+1)(β3+1) |
| 1 |
| (α20+1)(β20+1) |
考点:根与系数的关系
专题:
分析:先由根与系数的关系得出αn+βn=-(n+1),αnβn=n2,那么
=
=
=
=
-
,再将
=
-
代入所求式子,化简即可求解.
| 1 |
| (αn+1)(βn+1) |
| 1 |
| αnβn+(αn+βn)+1 |
| 1 |
| n2-(n+1)+1 |
| 1 |
| n2-n |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| (αn+1)(βn+1) |
| 1 |
| n-1 |
| 1 |
| n |
解答:解:∵方程x2+(n+1)x+n2=0的两根为αn、βn,
∴αn+βn=-(n+1),αnβn=n2,
∴
=
=
=
=
-
,
∴原式=(1-
)+(
-
)+…+(
-
)
=1-
=
.
∴αn+βn=-(n+1),αnβn=n2,
∴
| 1 |
| (αn+1)(βn+1) |
| 1 |
| αnβn+(αn+βn)+1 |
| 1 |
| n2-(n+1)+1 |
| 1 |
| n2-n |
| 1 |
| n-1 |
| 1 |
| n |
∴原式=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 19 |
| 1 |
| 20 |
=1-
| 1 |
| 20 |
=
| 19 |
| 20 |
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
若a2=9,b3=8,则a+b的值为( )
| A、5 | B、-5 |
| C、5或-5 | D、5或-1 |

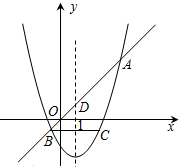 如图,抛物线y=
如图,抛物线y=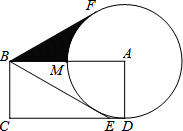 如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.
如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.