题目内容
 在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD.
在梯形ABCD中,AD∥BC,对角线AC=5,BD=12,AD+BC=13.求证:AC⊥BD.考点:勾股定理的逆定理,梯形
专题:证明题
分析:首先过点D作DK∥AC交BC的延长线于K,易得四边形ACKD是平行四边形,根据平行四边形的对边相等,易求得BD2+DK2=BK2,即可得△BDK是直角三角形,∠BDK=90°,继而证得AC⊥BD.
解答: 证明:过点D作DK∥AC交BC的延长线于K,
证明:过点D作DK∥AC交BC的延长线于K,
∵AD∥BC,
∴四边形ACKD是平行四边形,
∴CK=AD,DK=AC=5,DK∥AC,
∴BK=CK+BC=AD+BC=13,
∴BD2+DK2=BK2,
∴△BDK是直角三角形,∠BDK=90°,
即DK⊥BD,
∴AC⊥BD.
 证明:过点D作DK∥AC交BC的延长线于K,
证明:过点D作DK∥AC交BC的延长线于K,∵AD∥BC,
∴四边形ACKD是平行四边形,
∴CK=AD,DK=AC=5,DK∥AC,
∴BK=CK+BC=AD+BC=13,
∴BD2+DK2=BK2,
∴△BDK是直角三角形,∠BDK=90°,
即DK⊥BD,
∴AC⊥BD.
点评:此题考查了勾股定理的逆定理,平行四边形的判定与性质,以及梯形的性质,难度适中,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,抛物线y=
如图,抛物线y=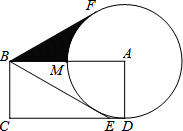 如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.
如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F.