题目内容
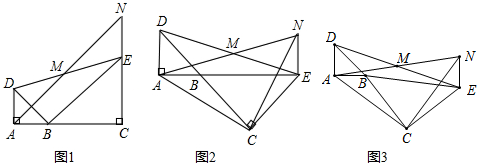
 在Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于点E,EF⊥AC于点F,求证:AC2=2EF2.
在Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC,DE⊥AB于点E,EF⊥AC于点F,求证:AC2=2EF2.考点:角平分线的性质,等腰直角三角形
专题:证明题
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,根据等腰直角三角形的性质可得∠BAC=45°,再判断出△AEF是等腰直角三角形,然后利用勾股定理列式整理即可得证.
解答:证明:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE,
∴AE=AC,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∵EF⊥AC,
∴△AEF是等腰直角三角形,
∴AE2=EF2+AF2=2EF2,
∴AC2=2EF2.
∴CD=DE,
∴AE=AC,
∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴∠BAC=45°,
∵EF⊥AC,
∴△AEF是等腰直角三角形,
∴AE2=EF2+AF2=2EF2,
∴AC2=2EF2.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,等腰直角三角形的判定与性质,勾股定理,熟记各性质并判断出等腰直角三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
对于函数y=-x2-2x-2,使得y随x的增大而增大的x的取值范围是( )
| A、x≥-1 | B、x≥0 |
| C、x≤0 | D、x≤-1 |
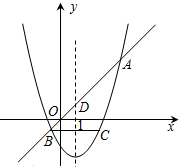 如图,抛物线y=
如图,抛物线y=